基础数学课23-向量空间模型
这一张,我们继续上一章关于向量空间的学习。不过在这里,我们需要知道向量空间模型和编程是如何挂上钩的。
我们虽然说了下向量的概念,以及向量的基本运算。这里我们继续延伸,说一下向量空间的概念。
首先给出一个定义,如果一个集合中任意两个数的加减乘除算法的结果仍然还在这个空间中,那么这就是一个域。而这样的一个作用域,常见于推荐算法的计算中。计算需要用到的,是向量相关的概念,比如向量的长度,向量之间的距离和夹角。
首先是计算向量之间的距离,一个向量可以对应到一个空间坐标系中的一个点,那么坐标系中的两个点的距离计算方式有很多种,这里我们说下常见的几个,曼哈顿距离,欧式距离,切比雪夫距离和闵可夫斯基距离。
首先是曼哈顿距离,这个计算公式的来源是美国曼哈顿中计算不同地区之间的驾驶距离。
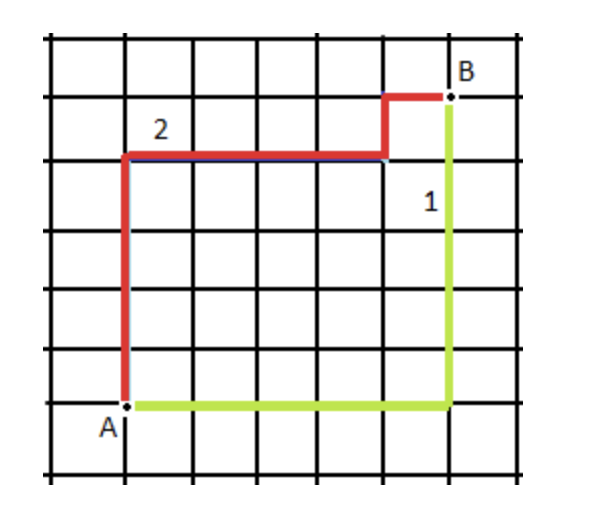
其中利用1或者2方法从A到B,其距离是一样的。
在一个二维空间中,这样的计算公式为
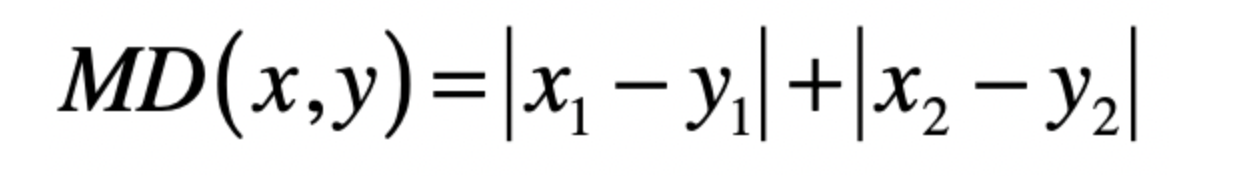
延伸到多维空间中,计算公式为
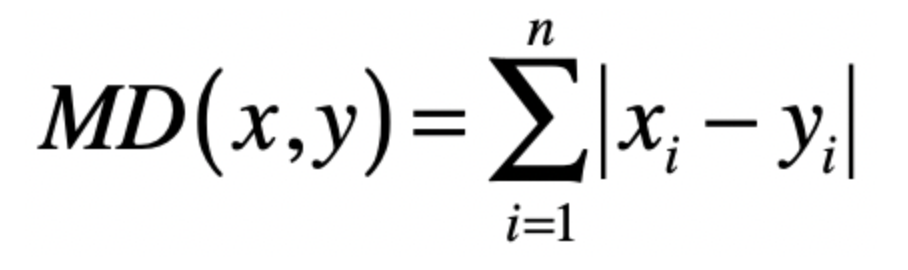
除此外是欧式距离,求两个点之间的真实距离。
比如在二维空间中,对应的公式为
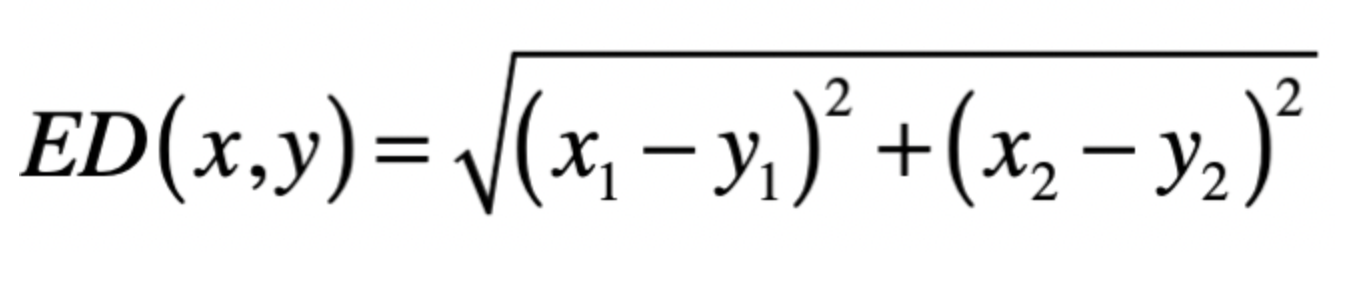
推广到n维空间,对应的公式为
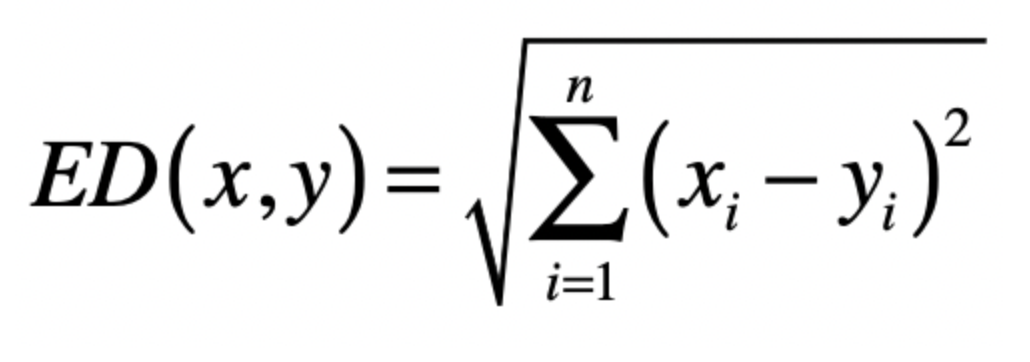
切比雪夫距离
一种模仿国际象棋的距离计算方式,棋子行走往往是斜线或者是沿着某个轴线以东,所以计算的方式为
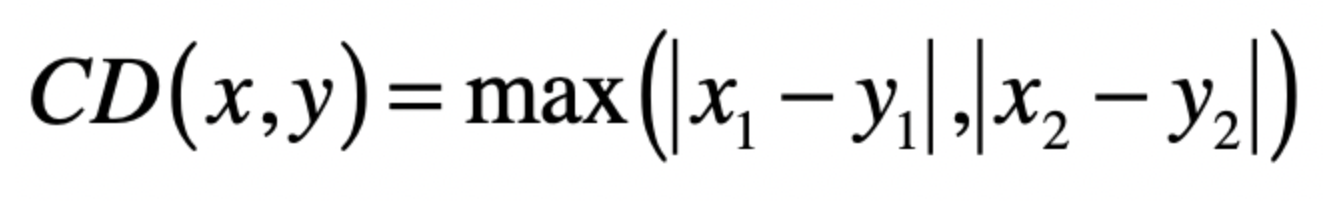
如果推广到n维空间,那么计算公式为
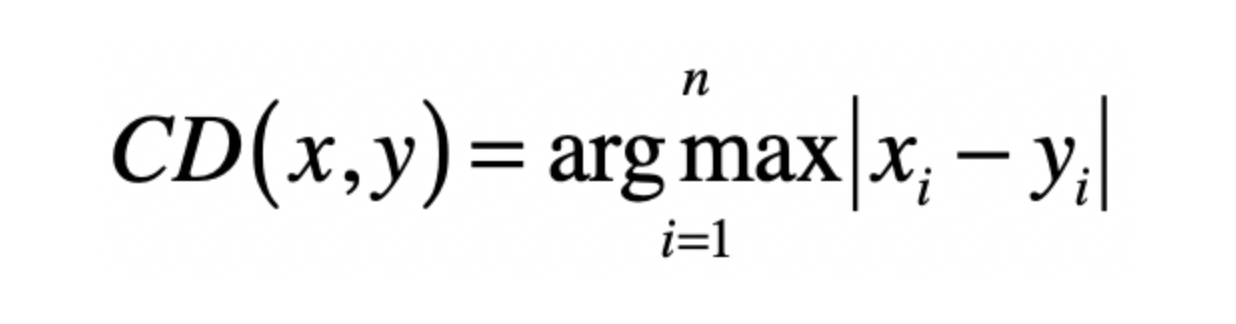
最后我们可以将这三种计算公式综合起来,形成一个如下的公式
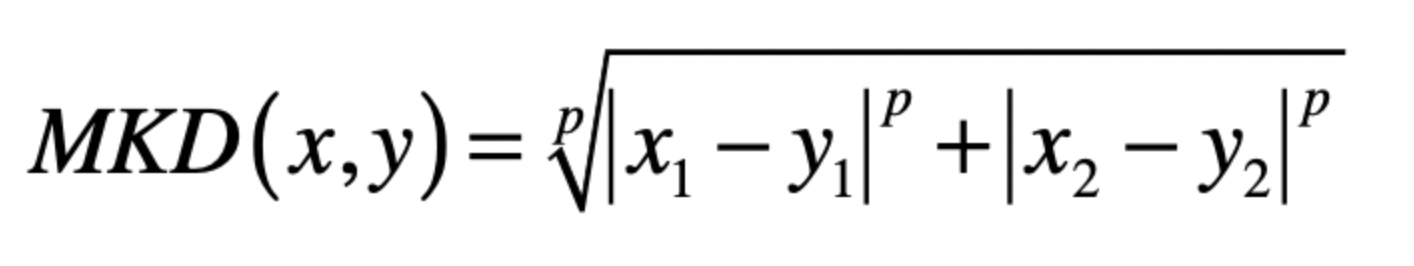
‘这个公式中p是一个可变参数,如果p为1,那么就是曼哈顿距离
如果p是2,那么就是欧式距离, 如果p到了无限大的取值,那么就是切比雪夫距离。
这个公式推广到n维的空间则可以如下
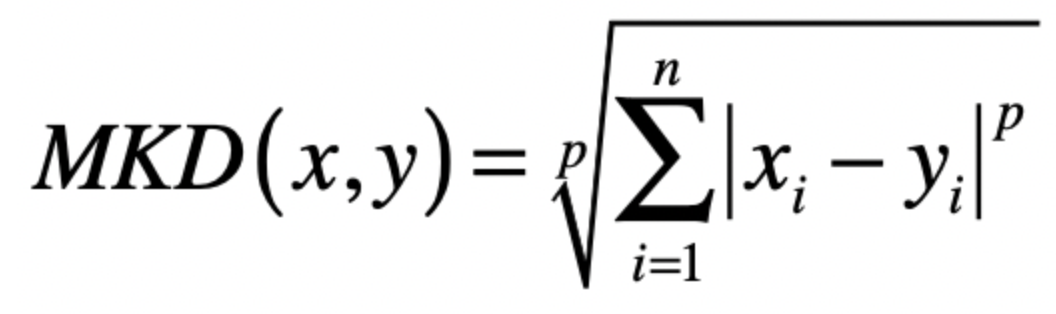
上面就是向量的距离计算
对于向量的长度,则更加简单,就是向量的点到空间原点的距离。
一般采用欧式距离来进行计算。
最后是向量之间的夹角
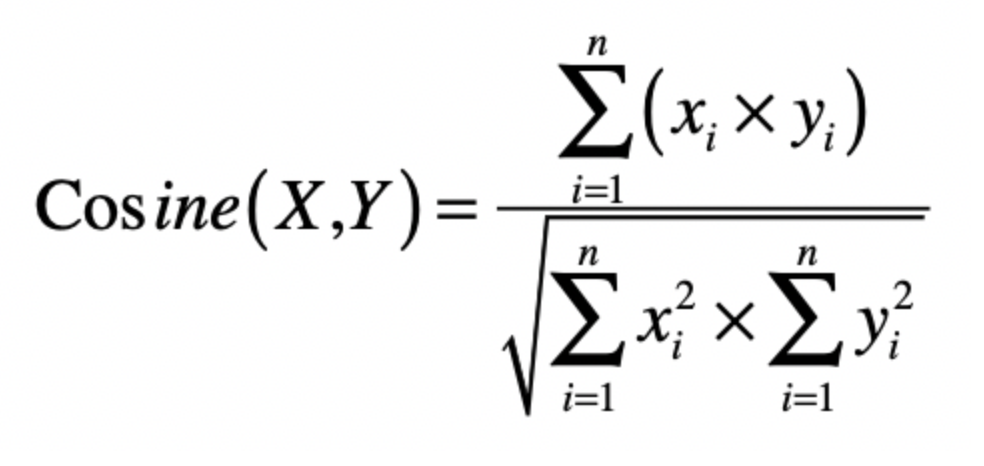
我们首先给出公式,其计算了两个空间向量形成的夹角的余弦值,具体公式如下
最终的取值范围是[-1,1]之间,如果重合时为1,如果完全相反则为-1
我们可以利用这个表明一个用户和一类用户画像的重合。
那么总结一下,向量空间模型理解起来就不难了
向量空间模型假设所有对象都可以转换为向量,然后根据计算向量之间的距离或夹角余弦来表示对象之间的相似程度。
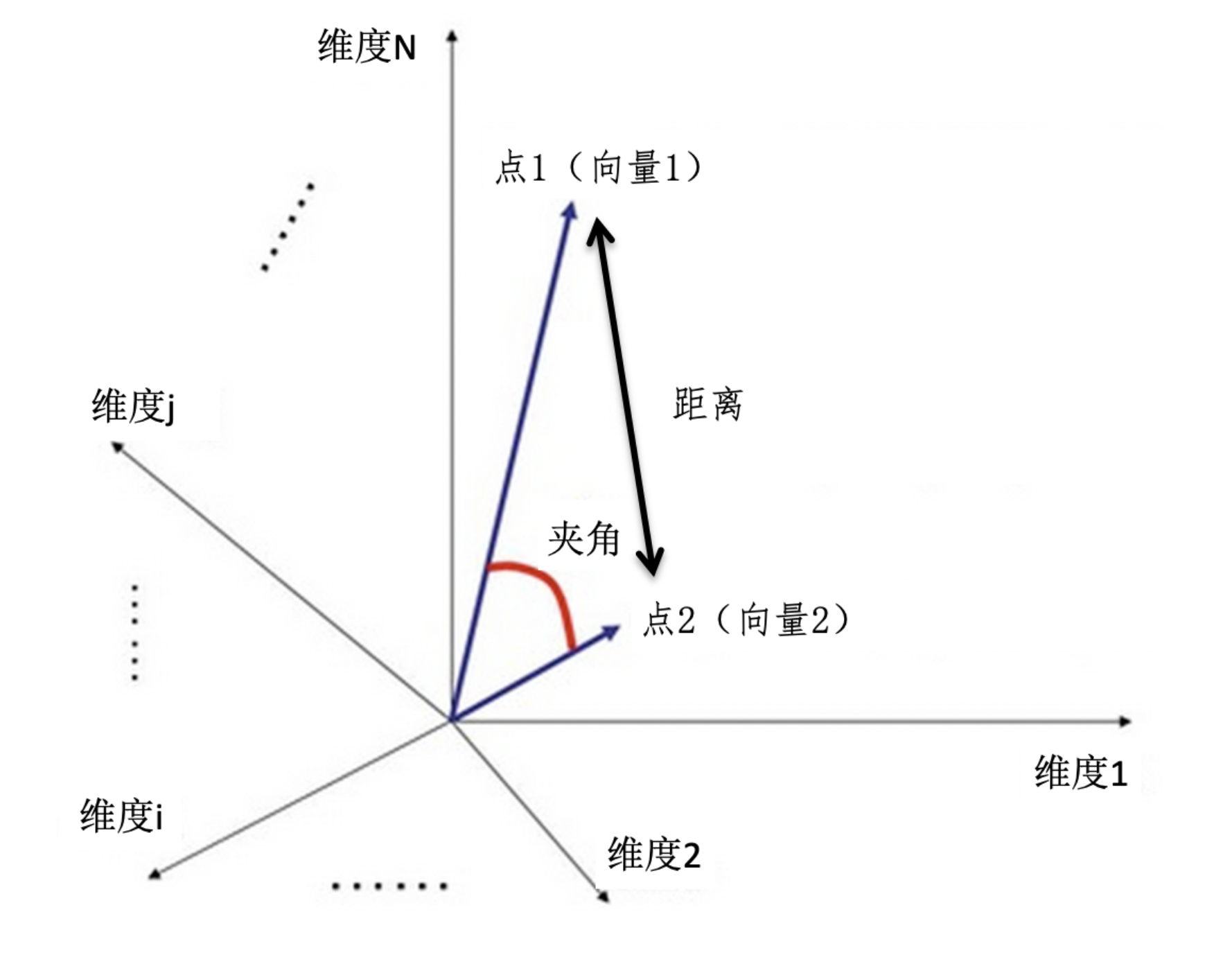
从而表示数据点之间的相似程度,现在也可以体现在相似度的机器学习算法。
比如K近邻,K均值等。