基础数学课22-线性代数
概率统计关注的是随机变量和概率分布,但是在实际工作中,不仅要关注单个变量之间的关系,还要进一步研究多个变量之间的关系。这就延伸到了线性代数。
而且线形代数,可以帮助我们计算很多日常生活中的问题,比如计算两个地点之间的距离。互联网中全部网页的PageRank。
那么这一章,我们作为开篇。先说下在线形代数中的常见概念。
- 向量
之前我们使用了数字来进行概念和统计的计算,而一个简单的数字属于标量。而不是向量,并不能表示方向。如果想要展示方向的话,就需要使用向量这个概念。向量利用一组数字,来展示方向等概念。就比如 x中 x1 x2 x3这样的一个一维数组,其中n就是向量的维度。
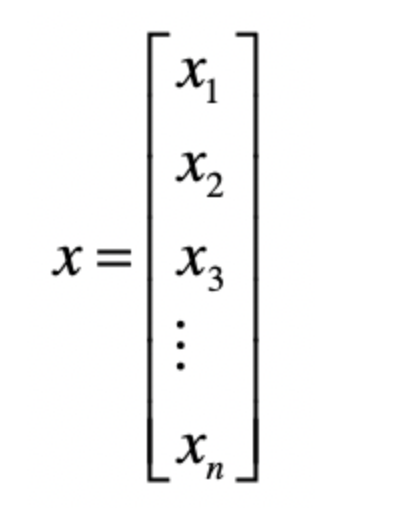
向量中出了数值的大小之外,还具有方向。那么如何展示方向呢?
如果我们将向量中某一个元素看作坐标轴的坐标,这个向量看作空间中的一个点。那么以原点是起点,以向量代表的点为终点,就能形成一条有向直线。利用这样一条直线,我们就可以进行向量空间,向量直角等概念的计算。
如果一个向量中包含了多个元素,就可以对应到机器学习中的特征转换,一个物体中的多个特征转换为向量中多个维度的值,每个元素就代表着一维特征,元素的值代表了对应特征的值。需要注意,这和矩阵的特征向量不一样,这个我们后续再说。
在有了向量的基本概念后,我们就可以对向量进行运算。这里分为了向量和标量如何计算,向量和向量如何计算。
向量和标量之间的计算,只需要将标量和向量中每个元素相加或者相乘就可以了,如果是向量和向量之间的计算,则需要进行额外处理。
如果是相加,首先需要确保其维度相同,比如一维数组的长度相等,然后进行相加。
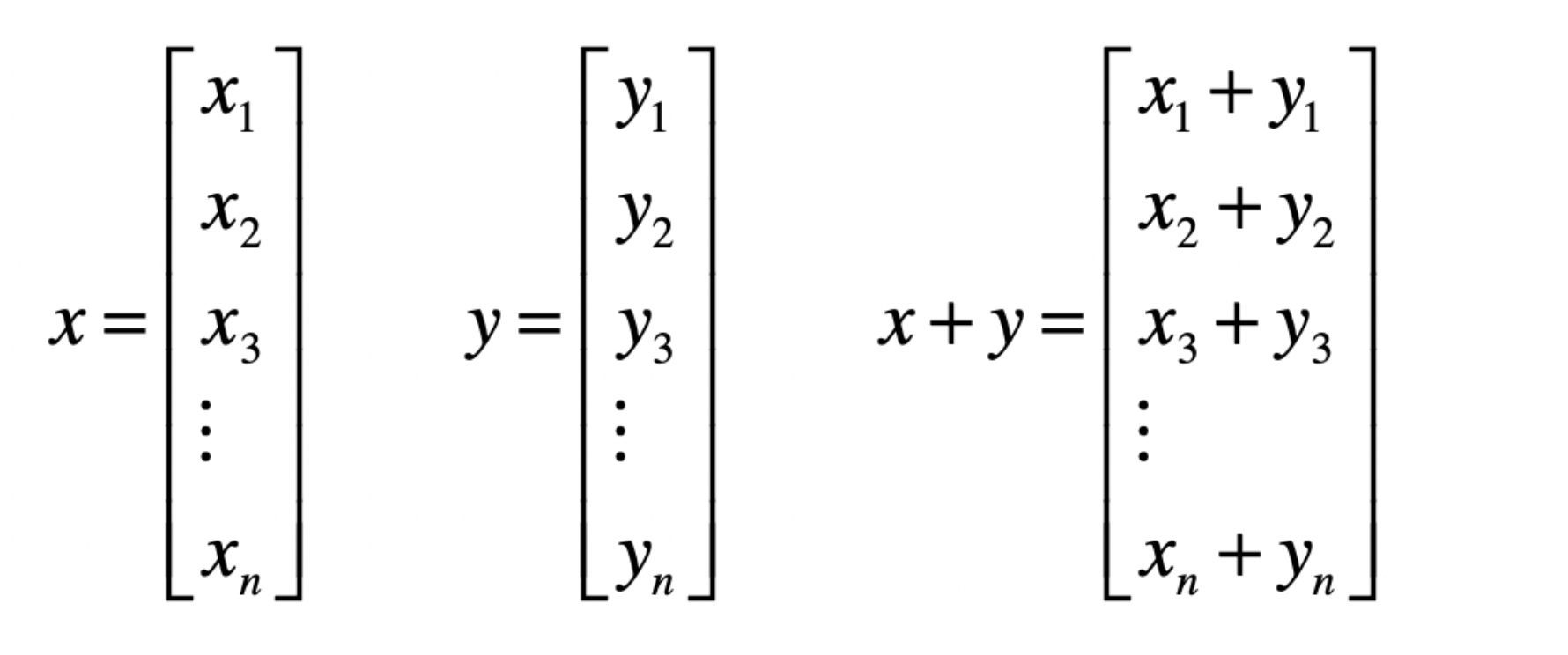
这样基本上运算可以如下。
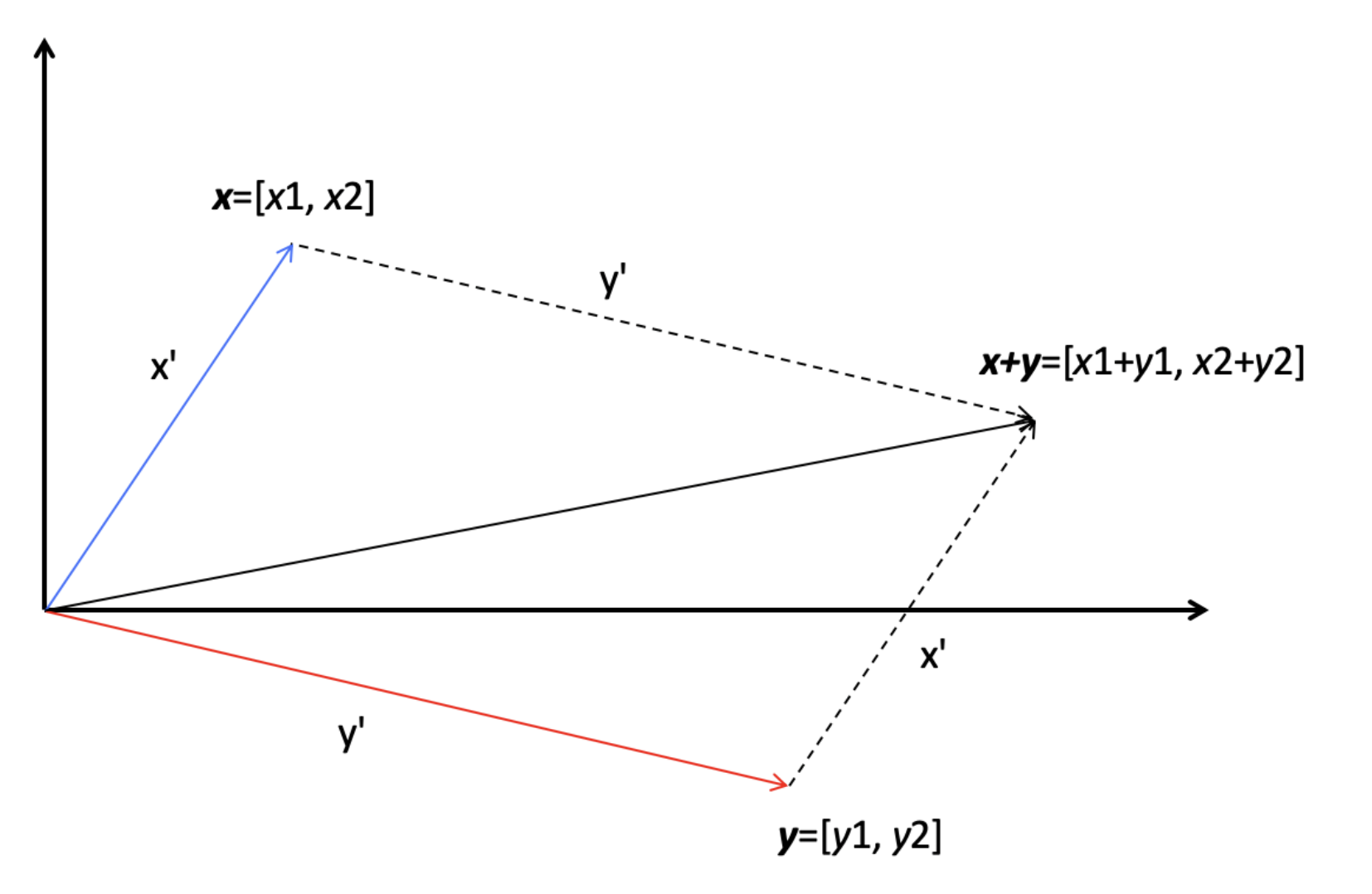
这就好比x向量沿着y向量的方向移动了y‘, y向量沿着x向量的方向移动了x’
然后是乘法,默认是点乘计算
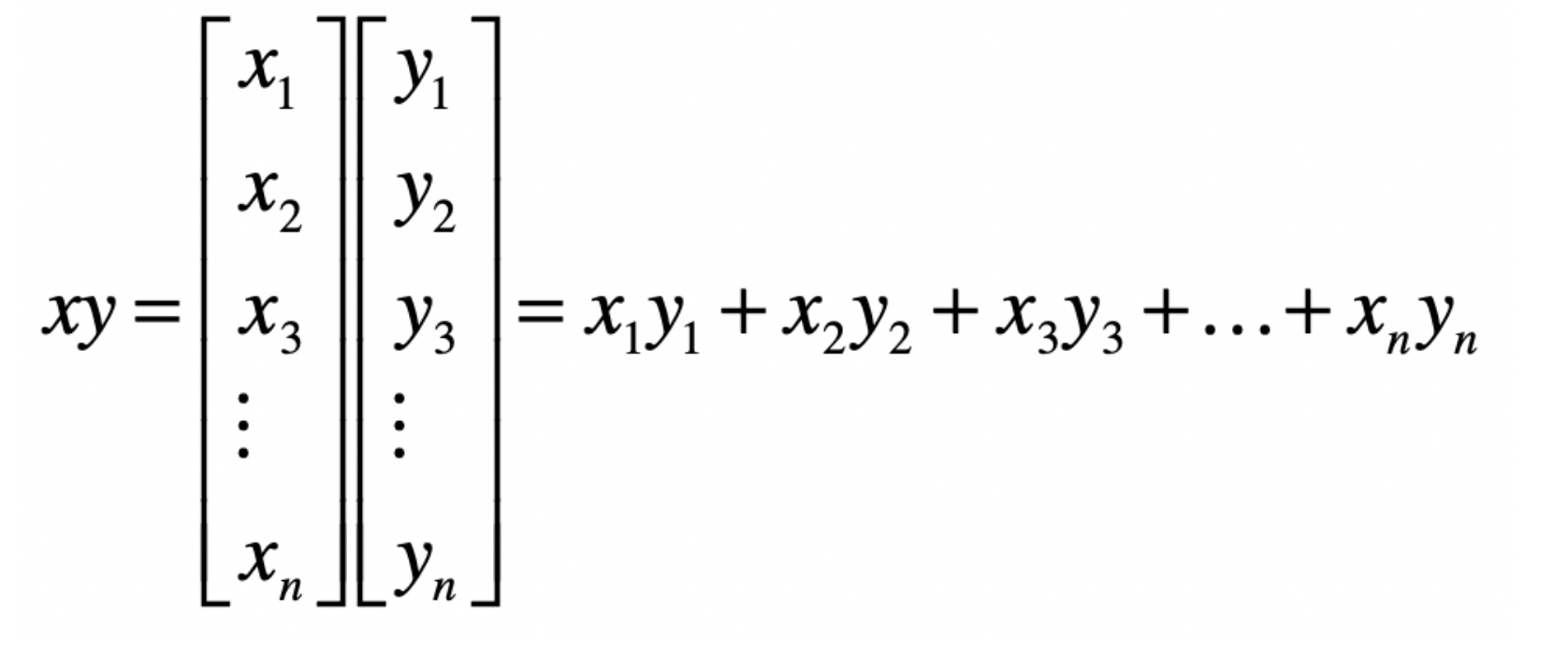
这样会把向量转换为标量。
其次是矩阵的计算,这里我们先简单说下,
矩阵由多个长度相等的向量组成,每列或者每行都是一个向量。我们理解,向量为一个一维数组,矩阵就是一个二维数组。
这里我们使用Xnm来表示矩阵,其中n和m是表示矩阵的行维度和列维度。
也就是n为每个子数组的长度,m为二维数组的长度。
如果是简单的加法,只需要确保n和m维度相同就可以了,然后将对应的元素两两相加就可以了。如果是乘法,则比较繁琐,写成公式可以为

关于这个公式,其实很好理解,就是矩阵的X的行向量,矩阵Y的列向量进行点乘。基本如下
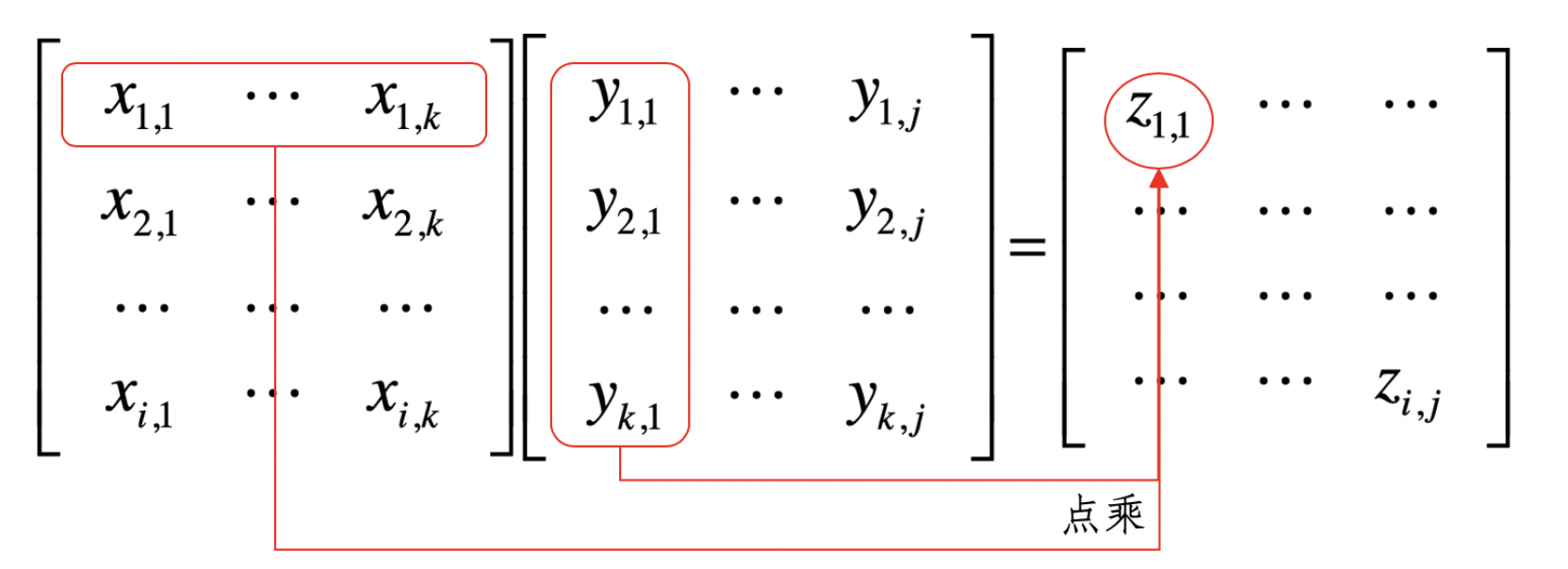
当然矩阵中的元素进行相乘,这种操作也是存在的,称为Hadamard乘积。但是用的比较少。
除此外还有些特殊操作,比如转置、求逆矩阵、求特征值和求奇异值等等。
转置就是将矩阵中元素的行索引和纵索引互换,例如Xij变为Xji,矩阵的形状由转置前的n*m变为转置后的m*n
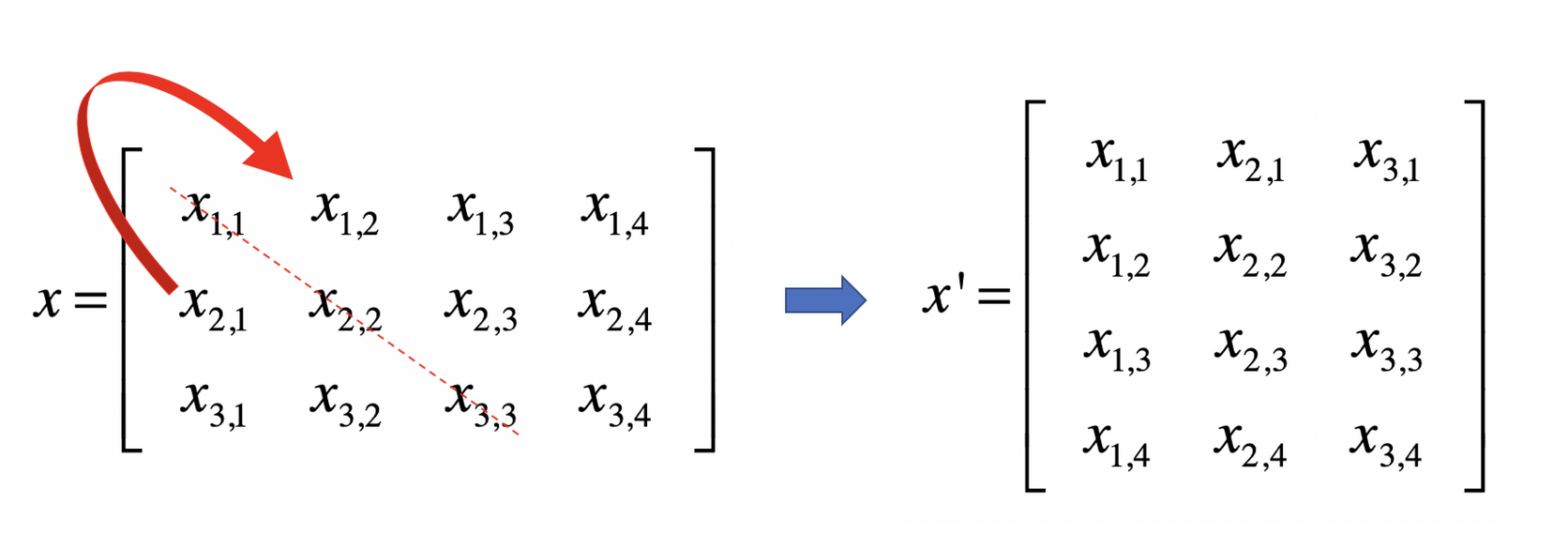
除了转置矩阵,还有一个概念就是逆矩阵,其本质上就是两个矩阵相乘得到一个单位矩阵,那么这两个矩阵中就有一个是逆矩阵。
而关于单位矩阵的概念,就是指的所有沿主对角线的元素都是1,其他元素都是0。
比如下图
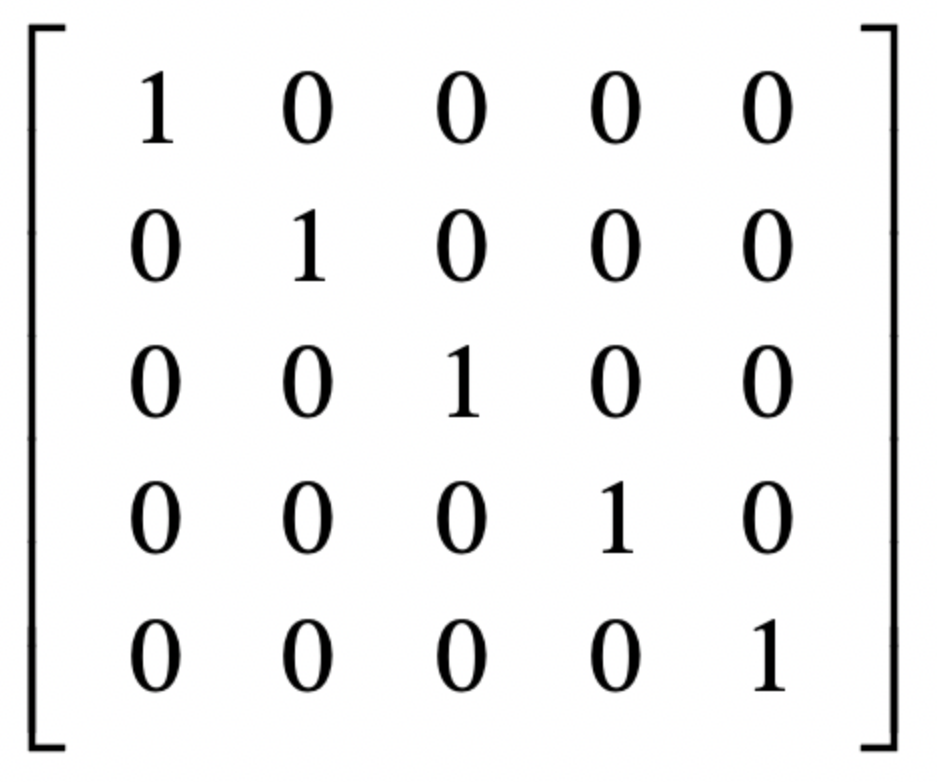
之后我们总结一下,我们说了标量和向量的区别,并说了向量的一些计算公式,无论是加法还是乘法,并说了点乘。