基础数学课21-概率和统计的总结篇
前面我们在说过了基本的计算机概念之后,讲了下在计算机中的概率和统计相关的概念。
这里我们进行下总结,总结之前,我们先带着一个疑问,为什么我们需要如此多的文档集合或者语料库来训练一个模型呢?
这就涉及到了拟合 欠拟合 过拟合这三个概念
对于每个学习模型来说,都有着自己的假设和参数,这里的参数说的是模型假设或者通过训练样本推导出的数据。比如贝叶斯的参数是各种先验概率和条件概率。决策树中的树结点。
然后拟合,就是通过模型的假设和训练样本,推测出详细的参数。然后我们就可以利用推测出的参数进行预测。比如下面我们有一些数据进行分布。
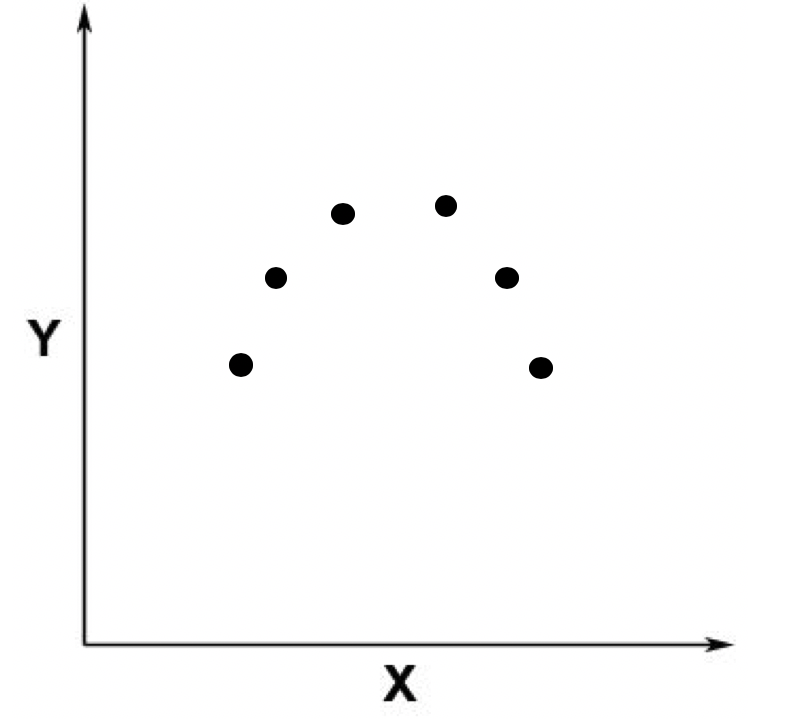
我们利用训练数据进行了训练得到了参数,得到的模型应该如下一条黑色曲线。
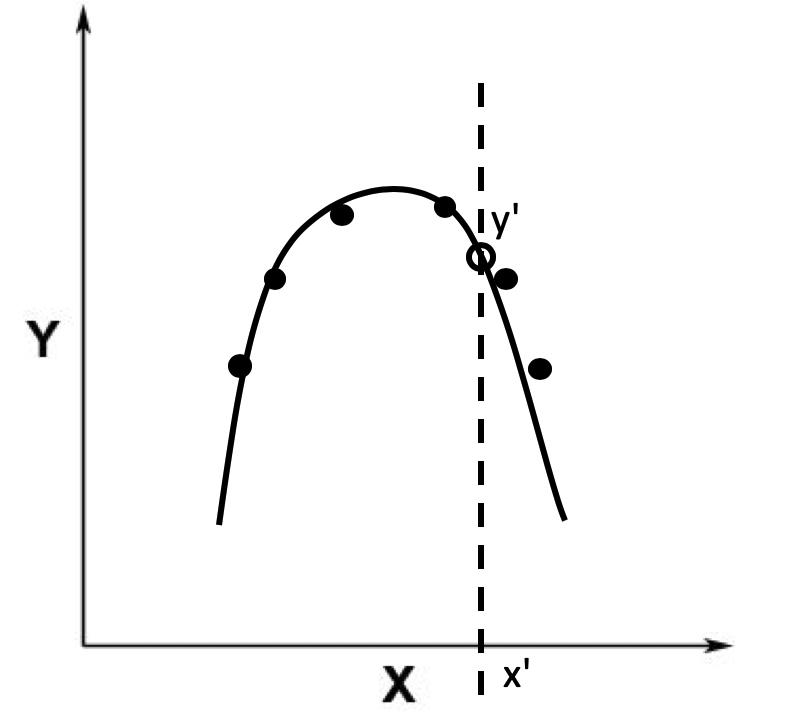
这里我们就可以利用这条曲线,来根据x轴的自变量,获取到对应y轴的因变量。
而且相对精准,这就是适度拟合。
但是有时候的模型太过简单,得到的误差比较大,这种情况就是欠拟合。
比如如下的黑色曲线,会得到差异较大的数据,这种情况就是欠拟合了吗,其中数据的差异就叫做偏差。
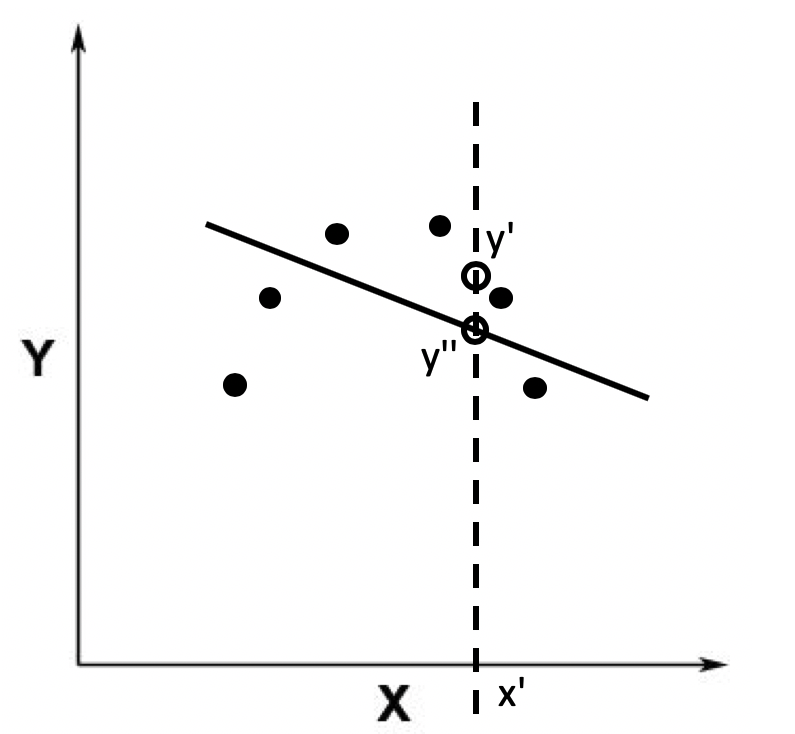
欠拟合说明了模型并不合适,同样的过拟合也是不合适,如果拟合得到的模型过于精密,导致和实际数据也会有冲突。
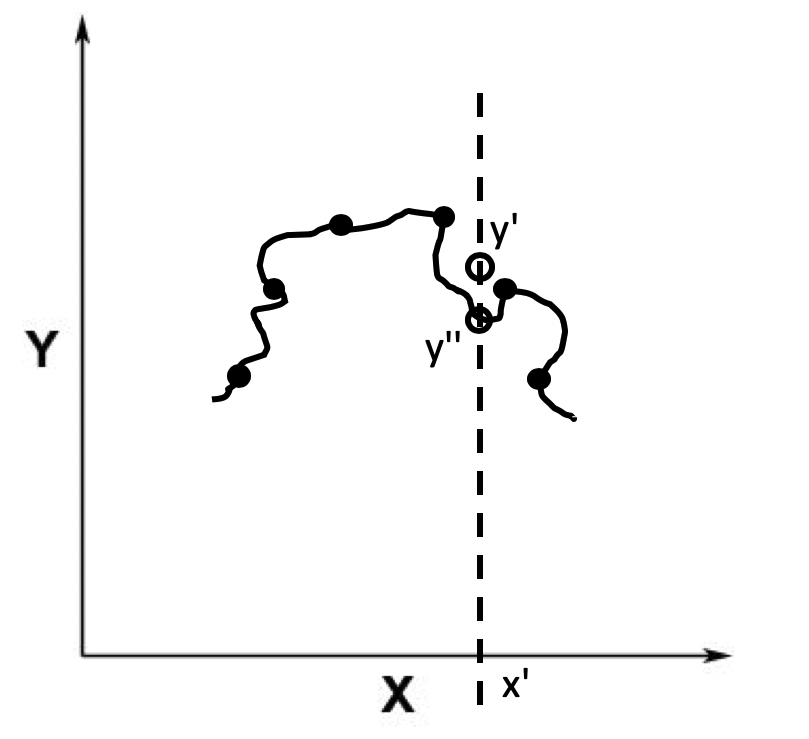
比如这条线,离数据点更加的近。但是在实际预测的时候,可能出现更大的偏差。
出现这种情况的原因,往往是因为训练样本和测试样本不一致导致的。
比如训练的数据是苹果和橙子,但是测试数据是西瓜。
这种差异,称为方差。
在常见的监督式学习中,适度拟合 欠拟合 过拟合三种状态是逐步演变的。
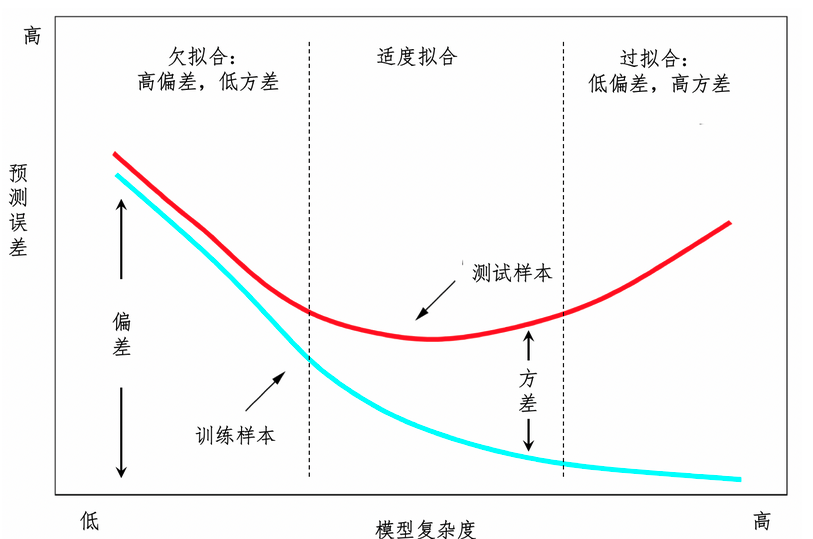
X轴表示了复杂程度,Y轴预测误差大小。
蓝色表示了在训练样本上的情况。红线则是测试样本中的情况。
这里看出,模型越复杂,越靠近训练样本,往往在测试样本中表现不好。因此我们希望找一个合适的,靠近中间的位置,也就是适度拟合的情况。
那么我们如何去处理欠拟合和过度拟合呢?
在解决这个问题之前,我们首先要高清楚产生这个问题的原因,欠拟合是因为特征太少,导致模型不够复杂。因此需要增加特征纬度,产生的样本具有更强的表达能力。
一开始我们说的朴素贝叶斯,其中重点是假设任何两个变量是相互独立的。这种假设在现实生活中往往不成立。所以朴素贝叶斯的表达能力有限,具有较大的方差。
因此采用二元或者三元乃至更大的N元文法来处理就可以。这就是增加特征来提高模型的复杂度。
相对应的,过拟合问题的原因是特征维度过多。太过于符合训练样本,无法适应测试样本或者新的数据。这种情况下,我们可以适当的减少训练的维度,比如剪枝。从而更好的适应数据的变化。
或者采用随机森林来进行构建,森林中存在很多决策树,不同树构建来源于同一个训练样本数据集。利用交叉验证的方式来保证训练数据和测试数据的一致性。每一颗树都拿出大部分数据进行建模,然后利用剩下的小部分进行预测。然后不断的划分训练数据集,训练出不同树。最终选择拟合好的模型。
在这里我们介绍了概率,统计中的常见概念
并说了 条件概率 联合概率 边缘概率三者的关系。
我们因此可以推断出贝叶斯定理。朴素贝叶斯定理。
并延伸出了多元文法,以及语言模型中的马尔科夫模型 隐马尔科夫模型。
从概率只是派生来的信息论,可以帮助我们设计机器学习的算法,比如决策树和特征选择。并利用数据分布来将特征转换为计算机可以理解的。利用假设检验验证模型。