基础数学课15-马尔科夫模型
我们研究了多元文法模型,但如果每个状态之间的转移是按照一定的概率进行的,就需要用到隐马尔科夫模型。
之前我们说过,语言模型中有一个马尔科夫假设,其中说,每个词的出现概率和前一个或多个词有关。如果是每个状态的出现概率只和前一个状态有关,这就被称为一阶马尔科夫模型或者马尔科夫链。
最简单的马尔科夫链可以形容为如下
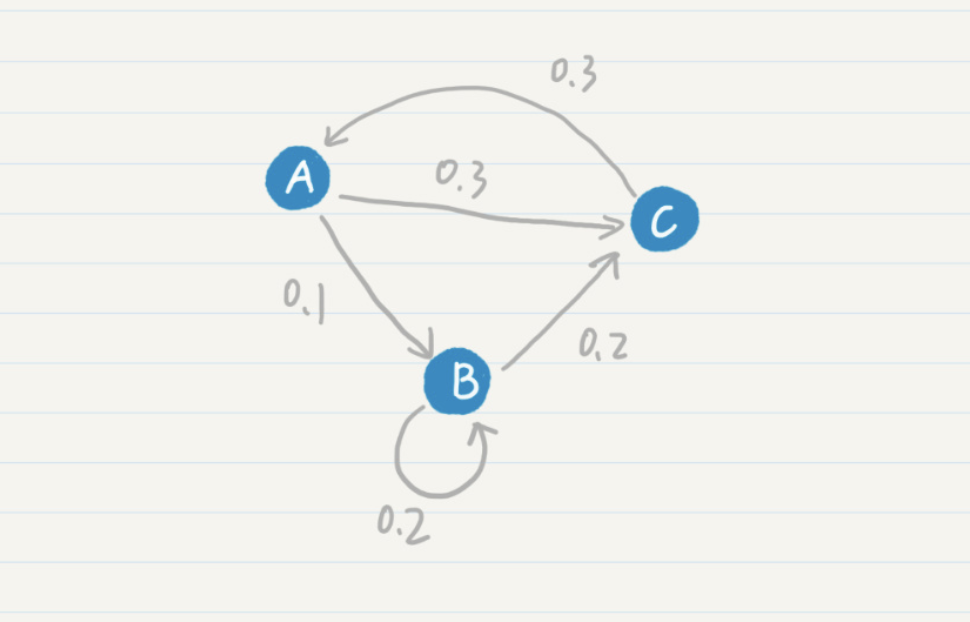
整体的状态转移如下表。
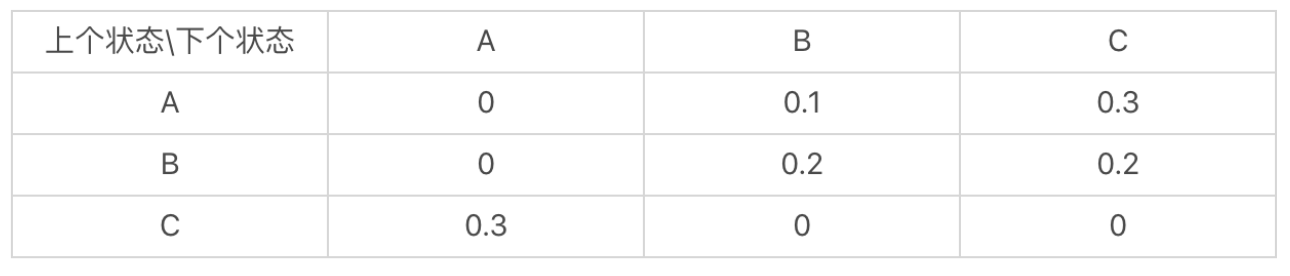
这里我们使用单词来替代上下状态
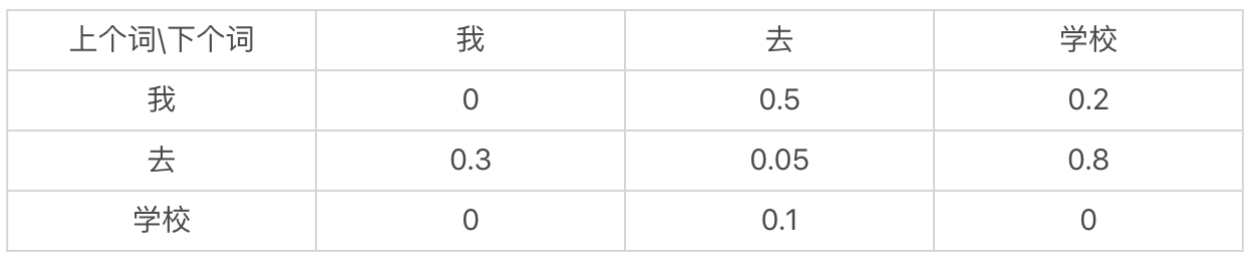
这里从学校转移到我的概率基本上就是0
那么隐马尔科夫模型就可以给语言识别进行使用。除此之外,在Google公司内部,还有着一个PageRank的链接分析算法,也是基于马尔科夫链。也就是冲浪者从某张页面触发,会从这个页面中的链接选择一个作为下一步的目标,理论上,可以永不停歇的冲浪,一直从图中走下去。
而随机访问中,越是频繁访问的链接,越是重要,所以越有概率被缓存或者打广告。
那么PageRank和马尔科夫链有什么关系,
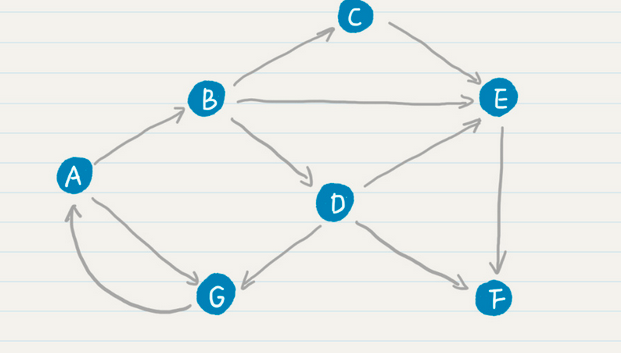
这里首先是一个web的拓扑图,在这个图上,和马尔科夫的状态转换类似。
在PageRank算法中,假设每个网页的出度都是一定的,比如1/3或者1/2,下个页面从这个页面转移过去的概率只和当前页面有关。满足了基本的一阶马尔科夫假设,除此外PageRank在标准的马尔科夫链之中引入了随机的跳转操作,也就是跳出马尔科夫链。最终形成了一个标准的公式
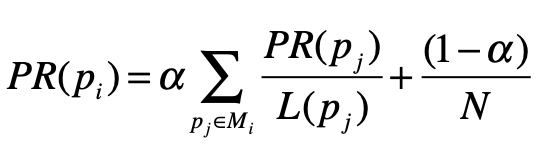
其中pi 表示第i个页面,mi是pi的入链集合,pi 表示第j个页面,PR(pj)是表示网页的pj的PageRank得分。L(pj)网页pj的出链接数量
除此外 a是用户不进行跳转的概率,N是网页数量。
除此外,我们还可以应用其到语音识别的过程
其主要利用的点是,语言的状态转换是具有概率的。
最经典的案例就是语音识别,利用概率来对语言进行识别的过程。
我们可以将每个等待识别的词来对应马尔科夫的一个状态。
虽然词有发音,但是对应的单词是哪个,计算机无法很好的准确确定,因为在人类语言中具有同音字。
比如,我要等你吗? 这里的吗,机器就需要知道是吗 还是妈
对于这种情况,就需要机器通过上下文进行推断。
这里就好比,机器知道某些信息,但是对于另一些信息并不知道,这些另一部分的信息就是实际该选择的字段。
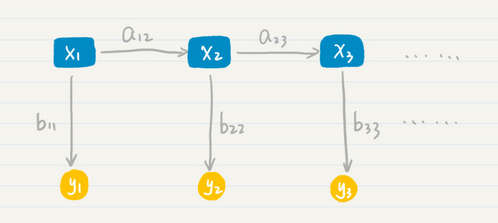
其中x1 x2 x3是隐藏层
A12 a23是从状态x1 到 状态x2 到x3 的的概率
B11 并是从状态x3到y3的输出概率。
那么这个最终结果的得出,由一系列的条件概率决定的,具体的公式为

这里为了方便理解,我拿一个例子举例。
比如如下的发音
Xiang mu kai fa shi jian
那么这个词组的的状态转移图可能如下
其可能包含 项目 开发 时间 这三个单词,其状态转移图如下

也有可能是 橡木 开发 事件
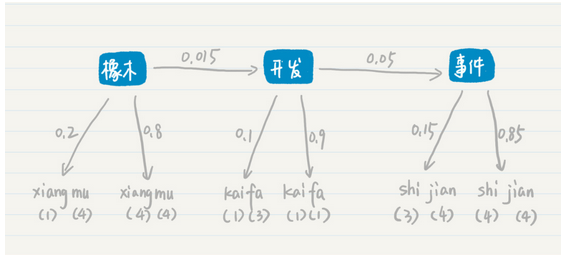
对于项目 开发 时间这个概率
我们可以选取 b中几率最大的事件和a中进行计算,带入上述的公式
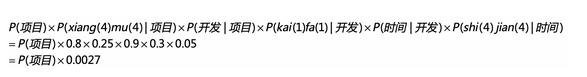
而 橡木 开发 时间则是类似
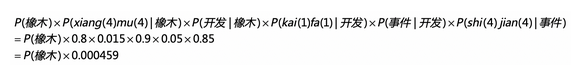
这种情况下,虽然单词识别得分相同,但是对于转换的概率来说,项目转开发的可能性更高。所以更加适合项目开发时间,这就是隐藏的状态层起到了关键的作用。
那么我们总结一下,马尔科夫模型考虑了n个状态之间的转换。其主要是根据每种状态及其之间的转换概率,求出出现的可能性,但是现实的场景更加复杂,观测到的不是状态本身,而是状态按照一定概率产生的输出。针对这种情况,隐马尔科夫提出了两层模型,也即为考虑状态转换的概率和状态产生输出的可能性。从而为语音识别提供了方案。