基础数学课14-简化概率模型
这里我们讲述下如何使用链式法则和马尔可夫假设来创建多元文法模型。
链式法则是概率轮中的常用法则。
其利用条件概率和边缘概率来推导联合概率。
![]()
这个公式的推导如下,利用了联合概率,条件概率,边缘概率的三角关系来进行制作的。
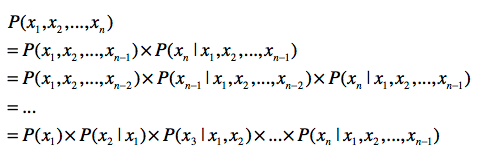
这样就介绍了联合概率如何进行拆分,形成众多子条件概率。
其次是马尔科夫假设,其假设在文本中,任何一个词的出现概率只和前面的1个或者若干个词有关,因此提出了多元文法,Ngram,其中N是任何一个词的出现,只和前面N-1个词有关
最为简单的就是二元文法模型,其概述为单个单词出现的概率只和前面1个单词有关
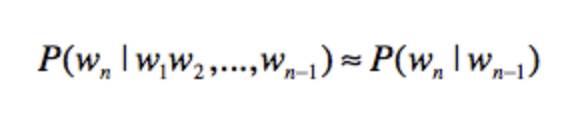
三元文法就是只和前面两个单词有关。
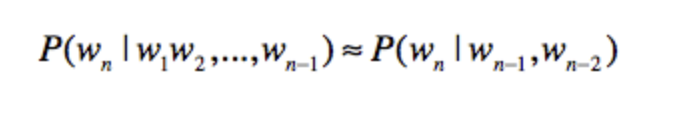
在了解了链式反应和马尔科夫假设之后,我们看下语言模型
假设我们有一个统计文本d,其中s是其中一个句子,内部包含一些单词 w1,w2,w3
我们想知道根据文档d的统计数据,语句s在文本中的文本出现的可能性
即P(d|s),但因为s由一系列的单词组成。所以我们的概率可以为
P(S|d) = P(w1, w2, w3……|d)
并因为我们的样本集在d中,所以可以写做
P(s)=P(w1, w2….wn)
我们再利用链式法则来把这个式子改写为
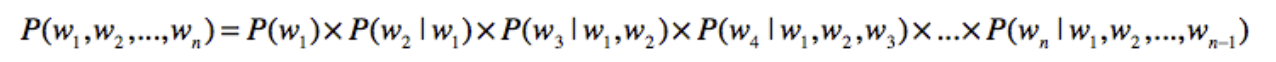
在获取到了这个链式法则之后,我们需要进行相关的计算,我们在其中,关于
P(w3,w1,w3)的出现概率就很低了,再往后的话,出现的概率就更低了,甚至趋近于0,我们虽然可以利用平滑的技巧,减少0概率的出现,不过这会导致最后的预测结果很差。
因此我们可以引入三元文法模型,将公式改为
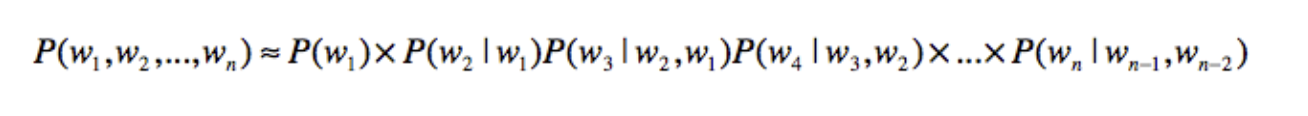
从而将复杂度改为了  这个数量级别。
这个数量级别。
这就是多元文法模型和链式法则在语言模型中的体现。
再之后就是语言模型的应用了。
比如就是信息检索,给定一个查询,哪个文档是相关的。
虽然我们可以采用布尔模型或者向量模型来解决,那么如果采用概率来进行计算呢。
最常见的做法是计算P(d|q)其中q表示一个查询,d表示一个文档
P(d|q)表达用户输入查询q的情况下,文档d的出现概率。
P(d|q)的结果可以是 P(q|d) * P(d) / P(q)
对于同一个查询,出现P(q)的概率是相同的,P(d)的概率是相同的,所以我们只需要计算P(q|d),也就是查询文档中是否存在类似的语句。
因此我们可以利用链式法则,将其重写为
![]()
再配合我们说的三元文法,最终可以得到
![]()
这样我们就可以对每一篇文档,获取查询对应的P(d|q)
其次可以应用于中文分词上,在中文分词上,由于语法,所以存在很多歧义,比如乒乓球拍卖完了,我们可以分词为 乒乓球 拍卖完了 乒乓 球拍 卖完了
对于这几种情况,我们就可以利用语言模型估算那种情况更加合理
如果整个文档是D,要分词的语句是s,分词结果就是w1,wn
那么我们求Ps|D的概率为
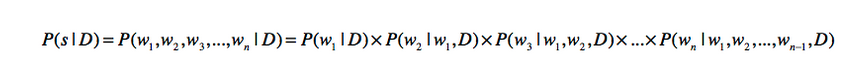
利用三元文法模型,将式子重写为
![]()
也就是语言模型可以估算不同分词结果在文档中出现的概率。
由于不同分词方式会导致w1 到 wn的不同,产生不同的PS,我们只需要取最大的Ps。就可以确定哪种分词更加合理。
那么我们总结一下,我们说了链式法则和马尔科夫假设,
并利用两者进行了推导。
首先是推导为链式反则
然后利用马尔科夫假设,将随机变量影响多的概率,转换为少的,
最后使用贝叶斯定理,进行推导。