基础数学课16-信息熵
接下来我们来说下信息论和一些基本的概念。
不过在此之前,我们先说下信息熵的概念。我们这里拿一个根据选择题确认武侠人物的小游戏举例子。
我们需要根据选择题来确认人物,而人物具有五个属性,设计五个题目来分别测试五个属性的对应值,然后根据组合值来确认最接近的任务。
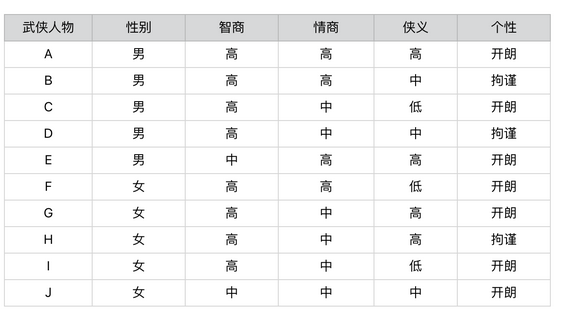
这个过程 很简单,但是在这个过程中,起决定性因素的环节是如何设计五道题。
比如题目的先后顺序会不会影响回答的问题数。
不同人物划分上是不是具有着不同的区分能力。
这里,信息熵主要就和区分能力挂钩,如果一个问题可以将不同分组的测试,更加清晰的划分到不同的分组,那我们就认为这个区分能力比较强。如果反之没法划分测试者。那么这个问题区分能力就认为比较弱。
这里我们分别看,性别和智商两个属性
性别可以直接将人划分为两个群体,且群体占比50%vs50%
而智商则是划分不同数量的群体,比如我们按照智商可以划分人群比例为0.8:0.2
那么其区分的能力就弱于性别的测试题。
而对于区分能力,如果采用科学的度量指标,就是信息熵和信息增益
信息熵就是给定集合的纯净度指标,比如一个集合的元素来源于同一个分组,那么就是即为纯净的,若来自于不同分组,那么熵必然大于0
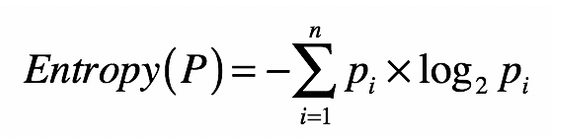
上面公式就是熵的公式,如果希望解释这个公式,需要从信息量说起。
这个公式主要就是计算某个随机变量的信息量期望,信息量就是信息论的一个度量,简单来说,我们观察到某个随机变量的具体值的时候,接收到了多少信息。事情发生的概率越大,产生的信息量越小;事情发生的概率越小,产生的信息量越大。
因此我们需要设计一个描述信息量的函数时候,需要考虑到以下特点
信息量应该是正数,一个事件的信息量和发生概率成反比。
所以得到的信息量的公式为 Hx = -logP(x),2 函数 函数log主要体现了Hx 和 Px的对数关系,这个公式可以量化随机变量的某种取值的时候,产生的信息量。最后加上计算随机变量不同可能性对应的期望,得到了熵的公式。
这里我们在解释一下公式,如果一个集合中的元素愈发趋近于后续落到同一个分组之中,那么信息量对应的就越小,如果元素愈发趋向于落入不同的分组之中,信息量就愈大,熵也就越大。
这里我们举个例子,如果一个集合里只有A组的元素,那么分组中A的出现概率是100%
所以这个集合的熵就是-100%*log(100%, 2) = 0。
但如果集合中有来自于A B组的元素,其中各占一半
熵就是2*(-50%*log(50%, 2)) = 1
这样可以看出,如果一个集合中分组越多,切分组足够均匀,熵值就越大,熵值代表了纯净的程度。
那么单个熵的值确定后,我们该如何计算整体的熵呢?
对于包含多个集合的更大集合,信息期望值可以根据多个小集合的信息期望值来推算,利用如下公式
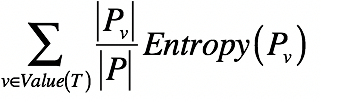
T是划分,Pv是划分后的小集合,EntropyPv表示某个小集合的熵, Pv/P表示某个小集合的概率。
因此对于多个小集合来说,整体的熵等于各个小集合的熵的加权平均,
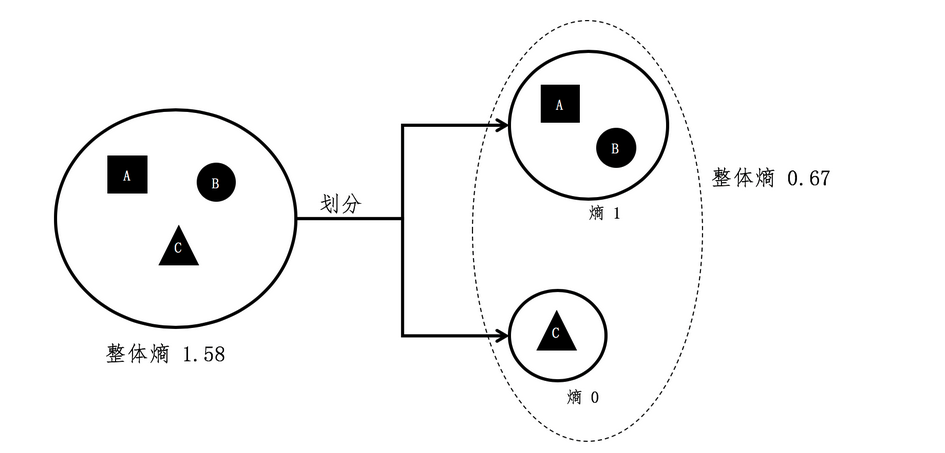
根据单个熵的计算,A B组组成的小集合,熵是1,C的熵是0
所以计算公式是
0.67*1+0.33*0 = 0.67
所以将划分后的整体熵和之前的进行对比,可以看出划分后熵小于之前的。*
如果这个划分有效的降低了熵,那么对于这种熵的下降,我们称为信息增益。
如果熵下降的越大,增益就越大。
故公式为
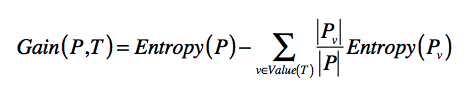
所以回到我们的武侠人物划分,如果一个问题的信息增益越高,那区分能力越高,信息含量就越高。
比如我们一开始所有人属于一个集合,所以熵为
10*(-1*0.1*log(0.1,2))=3.32
再之后,我们根据性别划分,假设每个小集合包含5种不同的人物分组,所以每个集合的熵为(-1*5*0.2*log(0.2,2))= 2.32,因此整体熵为0.5 * 2.32 + 0.5 * 2.32 = 2.32
最后信息增益是 3.32-2.32=1
而如果使用智商,则是划分为8:2
因此为(-1* 8 * 0.125 * log(0.125, 2)) 和 (-1* 2 * 0.5 * log(0.5, 2)) = 1
整体熵为 0.8 * 3 + 0.2 * 1 = 2.6
得到的信息增益是3.32 – 2.6 = 0.72
所以关于性别的区分能力更强。
那么总结一下,我们从人物性格测试开始,说了信息熵和信息增益,其中信息熵的计算基于集合各组元素分布的概率进行的。信息增益是集合划分前后的整体熵的差值,我们可以根据信息增益来选择最合适的测试题。