基础数学课17-决策树
我们在解释了信息熵和信息增益的概念之后,那么在回答问题后,就会被细分到不同的集合,在不断的细分下,熵会不断下降,最后被测试人员都得到了对应的人物。
在上次之中,根据信息熵来挑选合适的问题,最简单的就是选择信息增益最高的问题。从而快速下降熵值。
如果第一个问题,选择不同的分类方式可以获得如下的不同信息增益值

那最优的就是选择侠义。
然后选择侠义作为第一题后,用户会被划分为3组
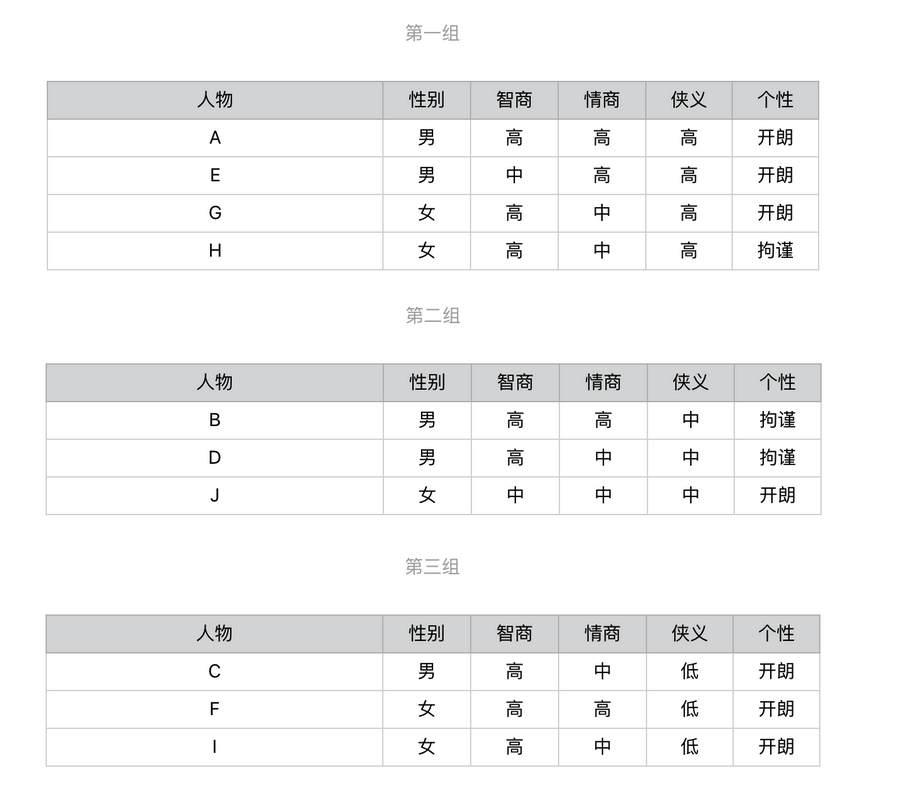
是否该继续计算不同分组中,信息增益最高的问题,根据计算的结果选择下一个问题,
如果我们不断的选择区分能力更强,增益最高的问题,可能只需要3个问题就能得到合适的人物,这一流程我归纳为了下图。
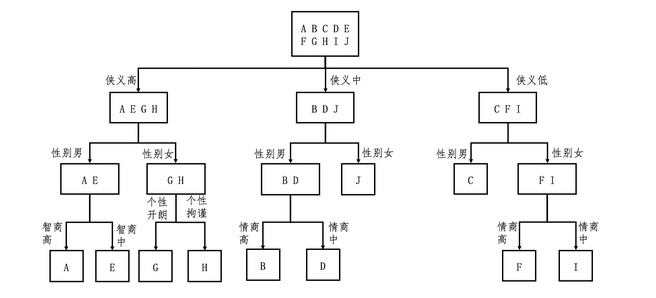
反之如果我们不选择熵值最高的问题,而是熵值最低的话,那么可能需要问完5个问题,才能确定武侠人物。
那么总结一下,如果想要高效的获取问卷调查,就是先根据分组人物情况,计算信息熵,以及熵值加权平均,获取到整个数据集的熵。然后根据其计算信息增益,选择区分能力最强的特征,进行细分。一直重复,直到所有样本都被分好了类。
在此基础上,人们发展出了很多优化版本的决策树,根据信息增益来构建的叫做ID3。其最显著的特点是,会考虑取值多的特征,因为如果能够将结果样本划分为更多更小的组,那么熵得分会更高,因此信息增益会上升。因此这样的结果树,会容易出现过拟合的情况
后续人们提出了C4.5算法
利用信息增益率来替代信息增益。信息增益率通过增加一个叫做分裂信息的项来避免取过多分组的特征。
其中计算规则如下
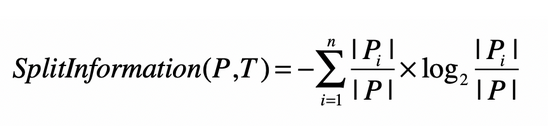
如果数据集P根据属性T划分了N个子数据集,Pi表示第i个子数据集的样本数。P是表示划分前的样本总量。看起来类似但并不相同。
熵只考虑数据集是否只是来自相同的分组。
分裂信息考虑的是子集的数量。因为特征多,所以子集数量多,所以分裂信息的值就越大。
所以在C4.5中,我们实际的值为
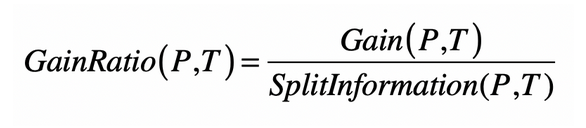
所以信息增益率的计算为信息增益/分裂信息。
除此外还有种决策树的算法为CART
其中采用基尼指数来进行特征选择。并且规避了ID3和C4.5算法中可能出现的根据特征属性划分数据,可能会划分出多个组,其采用了二叉树的方式,将数据划分为两份。方便计算。
基尼指数类似信息增益,如果集合中包含的子分组数量越多,基尼指数就越高。
那么我们总结一下,我们对信息增益如何应用为决策树进行了探讨。
并且说了信息增益进行训练的话,容易出现过拟合的问题。
所以人们提出了优化方案。