虽然前面学习了二叉查找树和数组的二分法查找,但是在很多时候,比如最坏的情况,性能还是极其的糟糕,极有可能出现单树过大的问题
引入了平衡二叉树,希望能保持二分查找法的平衡性,让树高为~lgN,
但这种维持完美平衡太难了,稍微放松下要求,能够在对数时间内完成数据结构
为了实现近似的平衡树
我们不再严格的苛刻二叉这一个条件,
开始允许树中的一个结点保存多个键,准确来说2-结点,3-结点
二叉树中结点2-结点(含有一个键和两个链接)
再引入3-结点 (含有两个键和三个链接)
2-结点 含有一个键和两个连接,左连接指向2-3树中的键小于该节点,右节点指向2-3树中的键大于该节点
3-结点,含有两个键和三个连接,左连接指向2-3树中的键小于该节点,中链接指向2-3树中的键都位于该节点两个键之间,右节点指向2-3树中的键大于该节点
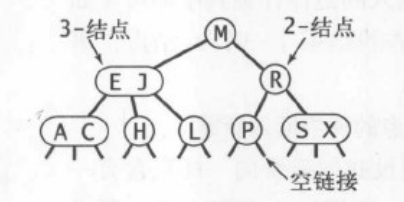
一个完美平衡的2-3查找树应该是所有空连接到根节点的距离相同
1.关于查找
2-3二叉树的查找和二叉树的查找方式一致
判断一个键是否在其中,就是先和根节点比对,然后根据大小递归去查找,同样如果为空查找未命中
2.关于插入
我们仍然选择的是进行一次未命中的查找,然后如果查找结束于2-结点,即把2-结点替换成3-结点
但是如果是一个-3结点的话,我们只能先创建一个-4结点,然后再转换成一个3个-2结点的2-3数,
一结点含有中值,一个结点含有最小值,一个结点含有最大值
中键变成了父节点,然后左右连接上面
为一个父节点为-2结点的-3结点连接呢
同上面我们会创建一个-4结点,但不会为中键创建为一个新节点,而是移动到之前父节点中,
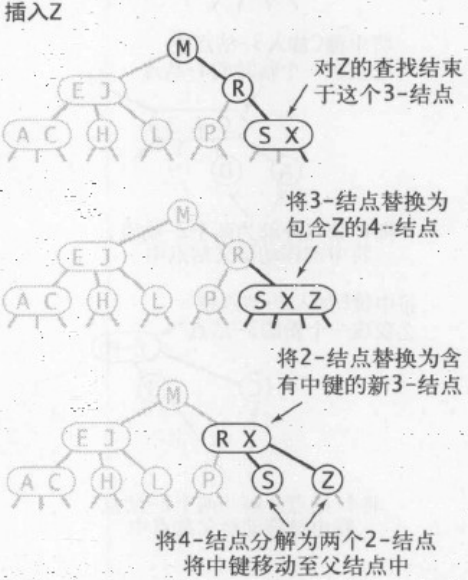
如果一个父节点也为-3结点的-3结点连接呢
那我如同上面,先构造一个-4结点,然后让中键上移至父节点,然后父节点再构造一个-4结点,然后一直让中键上移
直至一个-2结点接受他
如果所有的结点都是-3结点怎么办?
那么最后根节点会变成一个-4结点,我们像只有-3结点的树插入新键的方法解决此问题
将-4结点分成三个-2结点,使树高+1
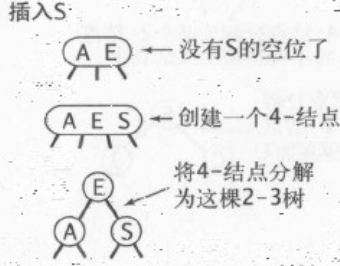
利用局部的改变,来最终引起全局的改变
最终,只有在根节点被分解为3个-2结点的时候,整个树高+1,所有的空连接到根节点的路径长度才会+1
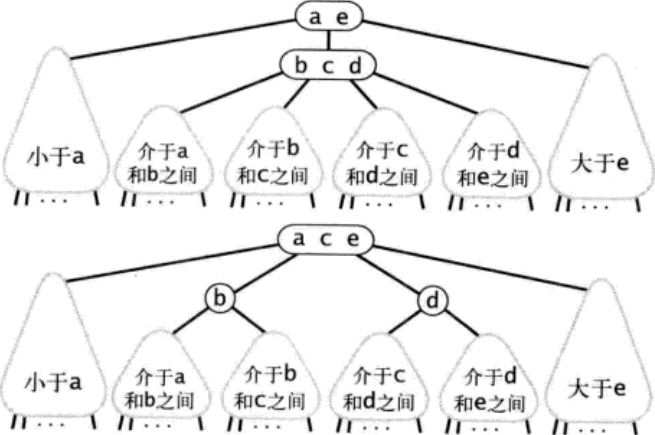
2-3树最大的不同,2-3的生长方式是由下往上生长的
一个完美平衡的二叉树的查找顺序是极其可怕的
含有10亿个结点的一颗2-3树的高度在19-30之间,我们只需要访问30次就能在10亿个键中进行查找插入