红黑二叉树的基本思想,使用标准二叉查找树,在此的基础上
利用红色连接将两个2-结点连接成为3-结点,其中一个2结点是另一个的左子节点.黑结点就是2-3树中的普通连接
这样的话,我们可以直接使用,二叉查找树中get方法
红黑树是含有红黑连接并且满足以下条件的二叉查找树\
红连接均为左连接
没有任何一个结点同时和两个红连接相联系
完美黑色平衡,任意节点连接到根节点的路径上的黑连接数量相同,(自底向上,无论走什么轮径,走过的黑连接数量都一致)

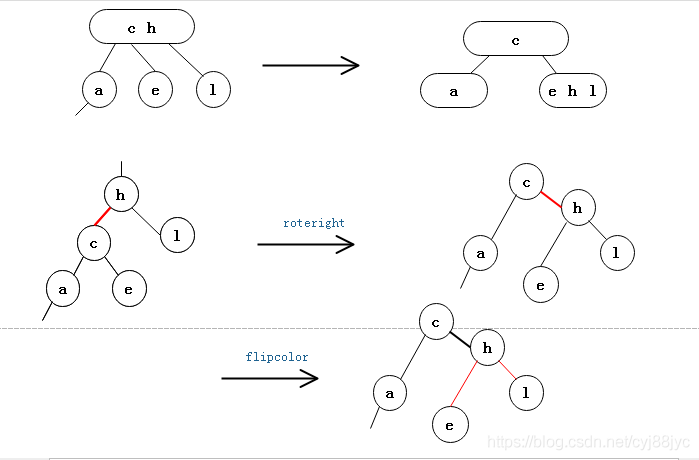
上面图中,横线都为红
具体实现如下
1.因为基本二叉树中,每一个结点都只有一个连接指向自己,故我们将颜色保存在Node数据类型的布尔类型变量color中
false为黑色,而且专门为此写一个isRed()方法来测试结点颜色
2.空链接为黑的
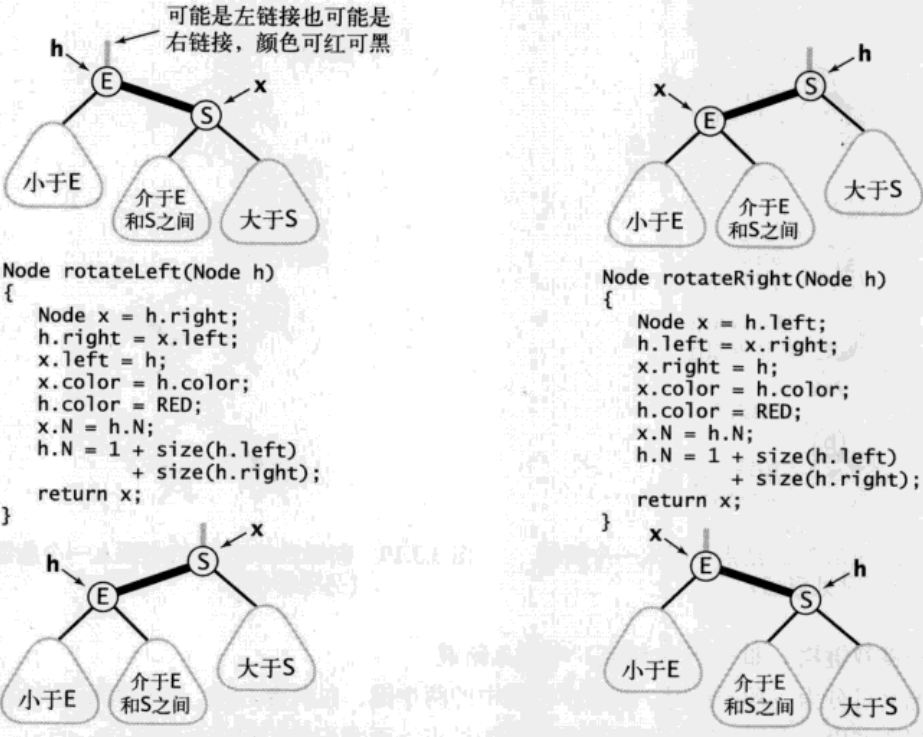
3.利用上面两个旋转方法进行旋转,以此来保持红黑树的性质-有序性和完美平衡
其左旋是将某个节点旋转为其右孩子的左孩子,而右旋是节点旋转为其左孩子的右孩子.
比如我们在只有一个键的树一个-2的结点插入一个键,使其变成一个-3的结点.
如果新键比旧键小,那么不需要任何操作,直接插入一个红色链接就行
如果新键比旧键大,那么需要在插入红色链接之后,调用之前 rotateLeft()方法旋转其红色连接使其变成上面的
同样在树底部的-2结点插入一个新键
那么同样,插入左边不必担心,直接使用,如果插入在右边(比其节点大),需要进行左旋转
在3结点插入新键的时候
分为新键最大,新键最小,和介于两者之间

通过这样的方式,我们让各种-3结点最后转化成-2结点,一个平衡的二叉树
在通过相同方式把其变成黑色
故创建一个方法filpColors();来转换一个结点中两个红子结点颜色为黑
同时再把父节点的黑色变红
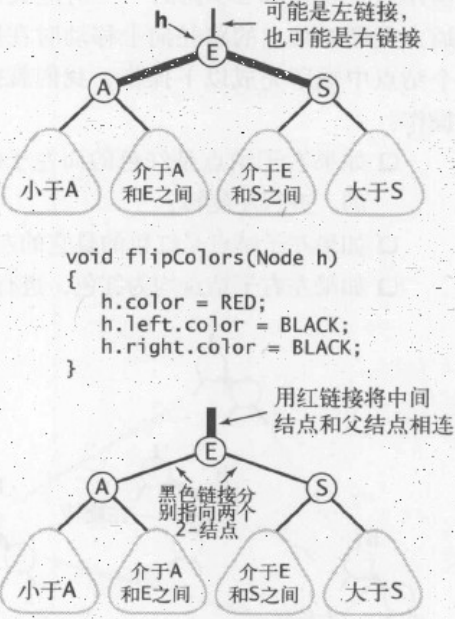
同样,如果根节点是红色,说明根节点是3-结点的一部分,
但是往往并非如此,我们每次插入后都会把根节点设置为黑色(故每次我们去插入数组,红色向上传递都会让根节点变红,然后再最后再把根节点再变回来,并且让树高度+1)
根节点由红变黑色就说明树的高度+1
我们分解3-结点,使其中间键上传,直到遇到-2结点,或者父节点
再上传的过程中,不断将其父节点设置为红的,作用同插入新节点
故我们一直进行左右转换,颜色转换这种方式,就可以一直保持红黑树结构
总结一下
如果右子节点是红色而左子节点为黑色的,进行左旋转
如果左子节点为红色的且它的左子节点也是红色,进行右旋转
左右子节点皆为红色的,进行颜色旋转
这方法和二叉树的put方法相似,但在最后进行了旋转操作,维持确定了红黑树的顺序
具体代码:https://github.com/HeavenXin/Data_Structure_Search/blob/master/RedBlackST.java
核心流程在于put中
private Node put(Node node, Key key, Value val) {
if (node == null) {// 如果为空
return new Node(key, val, 1, Red);// 返回一个新Node
}
// 仍然采用递归的方式
int tmp = node.key.compareTo(key);// 进行比较
if (tmp > 0) {
node.left = put(node.left, key, val);
} else if (tmp < 0) {
node.right = put(node.right, key, val);// 递归向下
} else
node.value = val; // 相同更新
if (isRed(node.right) && !(isRed(node.left))) {// 如果右子节点是红色而左子节点为黑色的
node = rotataLeft(node);// 进行左旋转
}
if (isRed(node.left) && isRed(node.left.left)) {// 如果左子节点为红色的且它的左子节点也是红色
node = rotataRight(node);// ,进行右旋转
}
if (isRed(node.left) && isRed(node.right)) {// 左右子节点皆为红色的
filpColors(node);
} // 这三次方式让其进行向上传递
node.N = size(node.left) + size(node.right) + 1;// 数量+1
return node;
}
然后是红黑树的删除
红黑树的删除也是比较困难理解的
如果直接删除,删除-2结点的话会留下一个空结点,一般情况下我们会将其替换为一个空链接(这样会破坏红黑树结构,因为从上面到根节点的黑连接不相同了)所以我们必须确保不删除一个-2结点
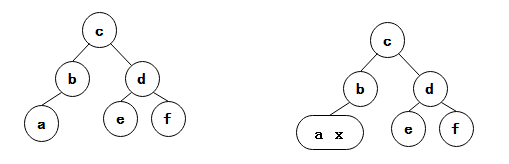
只删除3节点,方便补位
所以删除最小键过程中检查每个左子节点,如果发现左子节点中只含有一个键则进行分裂的逆操作,把该节点再添加一个键,这样在删除最小键后,节点不会为空,从而保持了树的平衡性。
那么,我们就需要考虑为左子节点添加一个键
分为三种情况
1.如果左子节点含有2个以上的键则不做操作,
2.如果左子节点只有一个键,而它的兄弟节点有2个以上的键,则从兄弟节点中借一个键过来
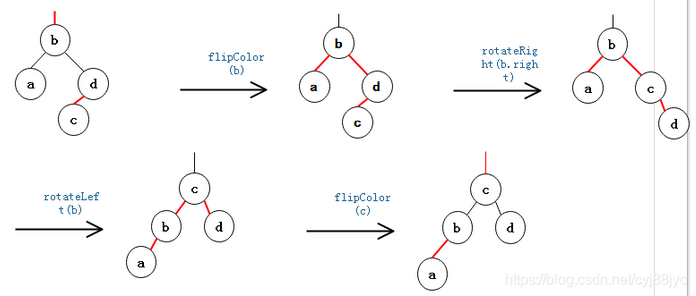
3.如果左子节点和兄弟节点都只有一个键,则从父节点借一个最小节点与左子节点和兄弟节点组合在一起
那么我们来看下最基础的删除最小键操作是如何实现的
public void deleteMin() {// 删除最小值
if (!isRed(root.left) && !isRed(root.right)) {
root.color = Red;// 如果左右子节点都是-2结点,可以将根为红结点
}
root = deleteMin(root);
root.color = Black;// 借完以后,我们将根节点的颜色复原
}
private Node deleteMin(Node x) {
if (x.left == null)
return null;
if (!isRed(x.left) && !isRed(x.left.left)) // 判断x的左节点是不是2-节点
x = moveRedLeft(x);
x.left = deleteMin(x.left);
return balance(x); // 解除临时组成的4-节点
}
对应的删除最大值的如下
最后的删除,则是结合了deleteMin/deleteMax和二叉查找树的delete操作
不断的查找,并且进行左移或者右移,确保代码无误
private Node delete(Node h, Key key) {
int tmp = key.compareTo(h.key);
if (tmp<0) { // 当目标键小于当前键的时候,我们做类似于寻找最小的操作,向树左边移动,合并父子结点来消除2-结点
if (h.left == null) {
return null;
}//为空直接返回
if (isRed(h.left) && !isRed(h.left.left)) {//是-2结点
h = moveRedLeft(h);//开借
}
h.left = delete(h.left, key);//递归
} else { // 当目标键大于当前键的时候,我们向右移动,并做与deleteMax相同的操作,
//如果相同的话,我们使用和二叉树的删除一样的操作,获取当前键的右子树的最小健,然后交换,并将目标键删除
if (isRed(h.left)) {
h = rotataRight(h);
}
if (key != h.key && h.right == null) { // 我们没有找到目标键,我们删除
return null;
}
if (!isRed(h.right) && isRed(h.right.left)) {
h = moveRedRight(h);
}
if (key == h.key) {//如果相同
h.value = get(h.right, min(h.right).key);//与其后驱交换
h.key = min(h.right).key;
h.right = deleteMin(h.right);//删除后驱
} else
h.right = delete(h.right, key);//都不满足,继续查找啊
}
return balance(h);
}