基础数学课31 实现一个推荐系统
这里我们利用一个知名数据集来实现一个推荐系统的核心模块的设计和实现
这里的知名数据集就是MovieLens,其中包含了四个文件,分别是ratings,movies,tags.links。其中的核心就是ratings,包含了四个字段,包括userId,movieId,rating,timestamp这几个字段,userId不必说,对于movieId则是电影的Id,rating则是用户对这个电影的评分。
那么我们主要就是利用协同过滤推荐算法进行用户和物品的匹配。
首先要对用户的评分进行一个标准化操作。
然后衡量一个用户和其他的用户或者物品的相似度。
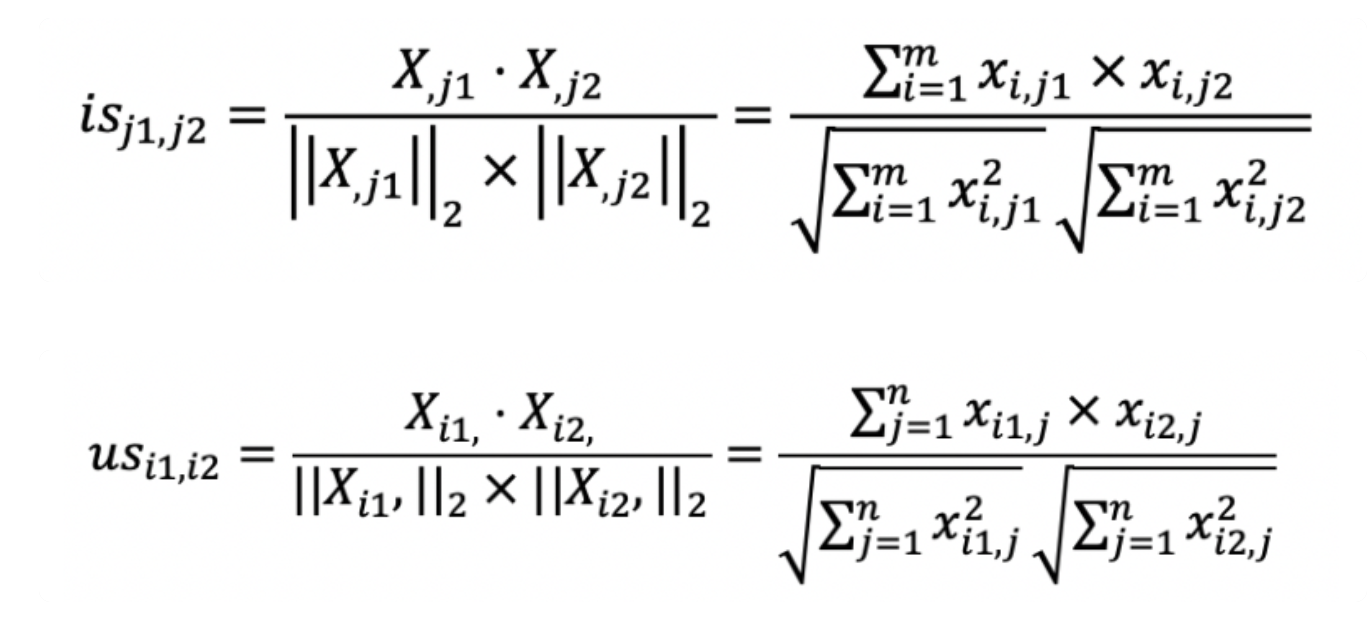
对于is系列,我们可以这么理解
首先我们有一个矩阵X,每一行是一个用户的喜好,每行的一个向量是某个用户的打分。
那么我们可以将X进行转置,形成X‘,其中以列区分用户,每列的一个向量是某个用户的打分。
这里我们将XX‘相乘得到结果Y,那么Y中的每一个元素就是用户i和j之间的喜好量结果,就是分子,如果i=j,也就是对角线上的一个元素,可以作为分母。
那么分子分母就存在了,我们就可以计算上述的公式


这样我们得到最终的矩阵后,利用用户之间的相似度,得到最终的得分P。
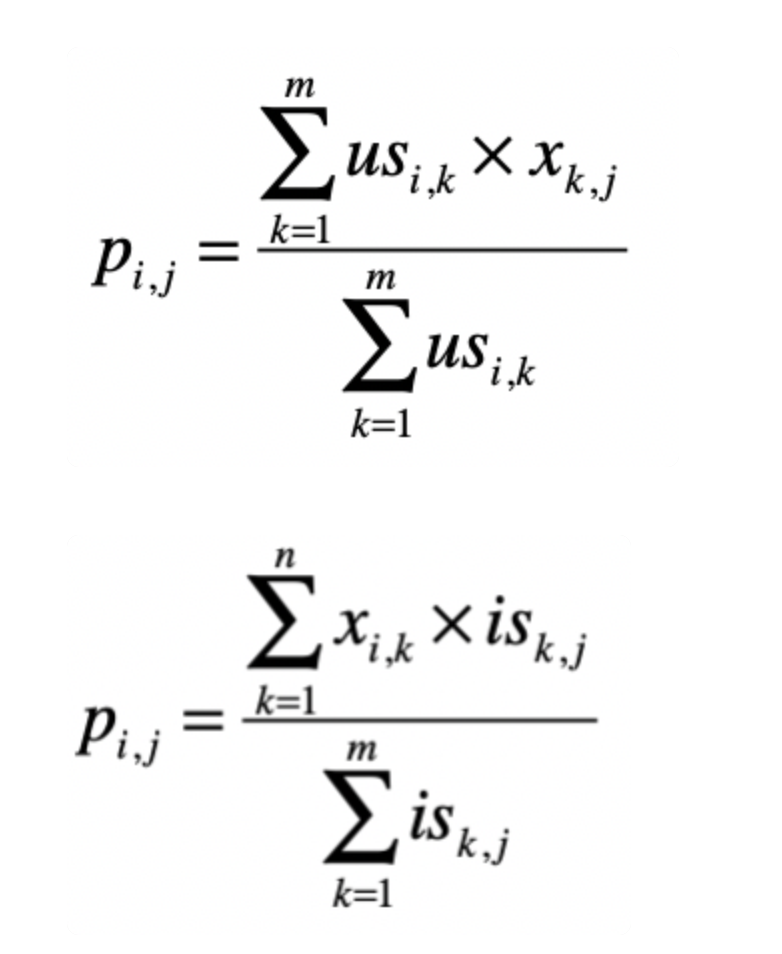
最终得到结果USP

按行相加得到USR
USP和USR相除。得到一个最终矩阵P

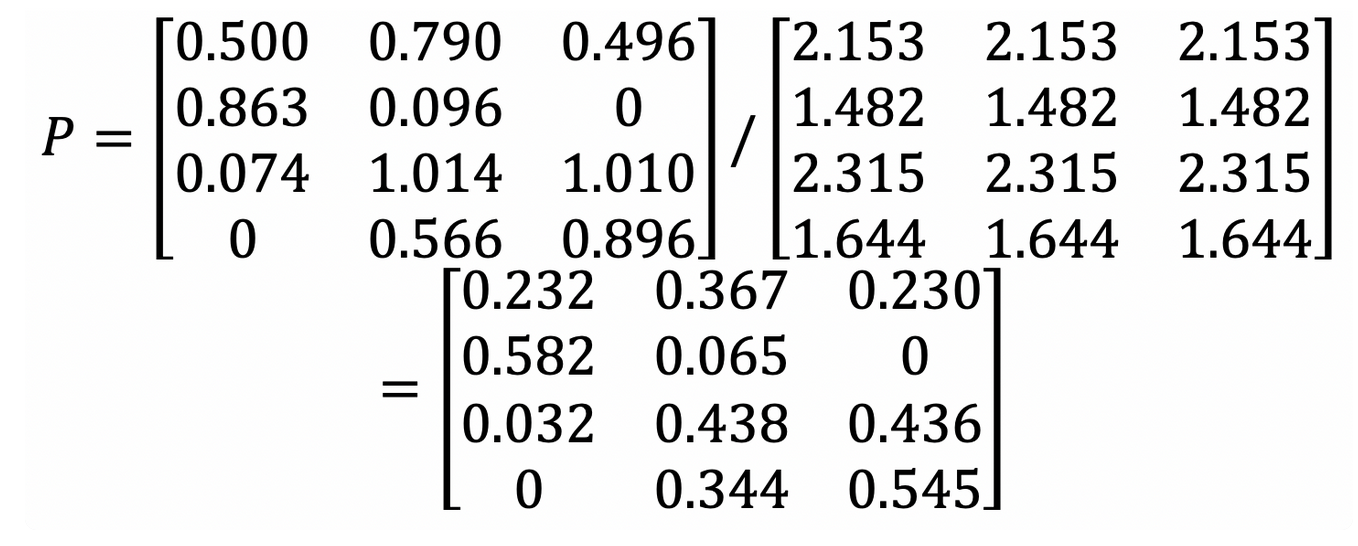
那么我们进行代码转换
|
import pandas as pd
from numpy import * # 加载用户对电影的评分数据 df = pd.read_csv(“/Users/shenhuang/Data/ml-latest-small/ratings.csv”) # 获取用户的数量和电影的数量 user_num = df[“userId”].max() movie_num = df[“movieId”].max() # 构造用户对电影的二元关系矩阵 user_rating = [[0.0] * movie_num for i in range(user_num)] i = 0 for index, row in df.iterrows(): # 获取每行的index、row # 由于用户和电影的ID都是从1开始,为了和Python的索引一致,减去1 userId = int(row[“userId”]) – 1 movieId = int(row[“movieId”]) – 1 # 设置用户对电影的评分 user_rating[userId][movieId] = row[“rating”] # 显示进度 i += 1 if i % 10000 == 0: print(i) # 把二维数组转化为矩阵 x = mat(user_rating) print(x) |
之后进行矩阵数据以行为维度进行标准化
|
# 标准化每位用户的评分数据
from sklearn.preprocessing import scale # 对每一行的数据,进行标准化 x_s = scale(x, with_mean=True, with_std=True, axis=1) print(“标准化后的矩阵:”, x_s) |
然后进行用户相似度矩阵的计算
|
# 获取XX’
y = x_s.dot(x_s.transpose()) print(“XX’的结果是’:”, y) # 获得用户相似度矩阵US us = [[0.0] * user_num for i in range(user_num)] for userId1 in range(user_num): for userId2 in range(user_num): # 通过矩阵Y中的元素,计算夹角余弦 us[userId1][userId2] = y[userId1][userId2] / sqrt((y[userId1][userId1] * y[userId2][userId2])) |
最后就可以进行协同过滤推荐了。
|
# 通过用户之间的相似度,计算USP矩阵
usp = mat(us).dot(x_s) # 求用于归一化的分母 usr = [0.0] * user_num for userId in range(user_num): usr[userId] = sum(us[userId]) # 进行元素对应的除法,完成归一化 p = divide(usp, mat(usr).transpose()) |
从而最后得到了推荐效果矩阵。
接下来我们还可以使用SVD算法来强化推荐策略
这里可以使用SVD分解来将原本的用户-电影两个级别转换为 电影-主题-用户三个界别,这里我们先回忆下SVD的定义。
如果一个矩阵X是对称的方阵,那么可以求的这个矩阵的特征值和特征向量。
其中具有n个特征值以及每一个特征值对应的特征向量。
此时X可以表示为X=VΣV-1
其中V是n*n个特征向量组成的n维矩阵,Σ则是以n个特征值为主对角线的n维矩阵。
但如果不是对称的矩阵,那么就不能直接分解,这时候就得使用SVD分解。
将X的转置X’ 和 X做矩阵乘法。得到n维矩阵X‘X,然后对这个得到的矩阵进行特征分解,得到n*n个特征向量,构建为一个矩阵V。
同样X和X‘做乘法。得到m维矩阵XX‘。进一步得到m*m个特征向量,构建为矩阵U
这样得到了两个向量矩阵,需要求的奇异值矩阵Σ。
这里我们先给出一个公式X=UΣV’
这里的奇异值矩阵代表着不同概念在文档集合中的不同重要程度,U代表了文档和概念的关系强弱。V代表着词条和概念的强弱。
对应到我们的系统中,就是电影到用户中区分的 主题 概念
其中主题就是科幻类,动作类这样的概念,
然后U表示用户对主题的热爱程度,V表示了电影和主题的关系。
这样进行的协同过滤。那么接下来我们就使用Python语言进行实现。
首先是构建矩阵
|
import pandas as pd
from numpy import * # 加载用户对电影的评分数据 df_ratings = pd.read_csv(“/Users/shenhuang/Data/ml-latest-small/ratings.csv”) # 获取用户的数量和电影的数量,这里我们只取前1/10来减小数据规模 user_num = int(df_ratings[“userId”].max() / 10) movie_num = int(df_ratings[“movieId”].max() / 10) # 构造用户对电影的二元关系矩阵 user_rating = [[0.0] * movie_num for i in range(user_num)] i = 0 for index, row in df_ratings.iterrows(): # 获取每行的index、row # 由于用户和电影的ID都是从1开始,为了和Python的索引一致,减去1 userId = int(row[“userId”]) – 1 movieId = int(row[“movieId”]) – 1 # 我们只取前1/10来减小数据规模 if (userId >= user_num) or (movieId >= movie_num): continue # 设置用户对电影的评分 user_rating[userId][movieId] = row[“rati |
然后将其标准化
之后使用numpy给出的svd函数
|
# 把二维数组转化为矩阵
x = mat(user_rating) # 标准化每位用户的评分数据 from sklearn.preprocessing import scale # 对每一行的数据,进行标准化 x_s = scale(x, with_mean=True, with_std=True, axis=1) print(“标准化后的矩阵:”, x_s # 进行SVD分解 from numpy import linalg as LA u,sigma,vt = LA.svd(x_s, full_matrices=False, compute_uv=True) print(“U矩阵:”, u) print(“Sigma奇异值:”, sigma) print(“V矩阵:”, vt) |
从而得到奇异值矩阵。
然后我们利用V来看下是不是分的合理。
|
# 加载电影元信息
df_movies = pd.read_csv(“/Users/shenhuang/Data/ml-latest-small/movies.csv”) dict_movies = {} for index, row in df_movies.iterrows(): # 获取每行的index、row dict_movies[row[“movieId”]] = “{0},{1}”.format(row[“title”], row[“genres”]) print(dict_movies) print(max(vt[1,:])) for i in range(movie_num): if (vt[1][i] > 0.1): print(i + 1, vt[1][i], dict_movies[i + 1]) |
从而查看是不是分组合适,这里我们看下相关的电影。
|
260 0.14287410901699643 Star Wars: Episode IV – A New Hope (1977),Action|Adventure|Sci-Fi
1196 0.1147295905497075 Star Wars: Episode V – The Empire Strikes Back (1980),Action|Adventure|Sci-Fi 1198 0.15453176747222075 Raiders of the Lost Ark (Indiana Jones and the Raiders of the Lost Ark) (1981),Action|Adventure 1210 0.10411193224648774 Star Wars: Episode VI – Return of the Jedi (1983),Action|Adventure|Sci-Fi 2571 0.17316444479201024 Matrix, The (1999),Action|Sci-Fi|Thriller 3578 0.1268370902126096 Gladiator (2000),Action|Adventure|Drama 4993 0.12445203514448012 Lord of the Rings: The Fellowship of the Ring, The (2001),Adventure|Fantasy 5952 0.12535012292041953 Lord of the Rings: The Two Towers, The (2002),Adventure|Fantasy 7153 0.10972312192709989 Lord of the Rings: The Return of the King, The (2003),Action|Adventure|Drama|Fantasy |
上述都是科幻类的电影,自然可以认为分类成功。
那么我们就通过SVD,实现了矩阵分解。
从而实现了基于主题的协同过滤。
最后贴上完整代码
|
import numpy
import pandas as pd from numpy import * from sklearn.preprocessing import scale # 加载用户对电影的评分数据 df_ratings = pd.read_csv(“./ratings.csv”) # 获取用户的数量和电影的数量,这里我们只取前1/10来减小数据规模 user_num = int(df_ratings[“userId”].max() / 10) movie_num = int(df_ratings[“movieId”].max() / 10) # 构造用户对电影的二元关系矩阵 user_rating = [[0.0] * movie_num for i in range(user_num)] i = 0 for index, row in df_ratings.iterrows(): # 获取每行的index、row # 由于用户和电影的ID都是从1开始,为了和Python的索引一致,减去1 userId = int(row[“userId”]) – 1 movieId = int(row[“movieId”]) – 1 # 我们只取前1/10来减小数据规模 if (userId >= user_num) or (movieId >= movie_num): continue # 设置用户对电影的评分 user_rating[userId][movieId] = row[“rating”] # 把二维数组转化为矩阵 x = numpy.asarray(user_rating) # 标准化每位用户的评分数据 # 对每一行的数据,进行标准化 x_s = scale(x, with_mean=True, with_std=True, axis=1) print(“标准化后的矩阵:”, x_s) from numpy import linalg as LA u, sigma, vt = LA.svd(x_s, full_matrices=False, compute_uv=True) print(“U矩阵:”, u) print(“Sigma奇异值:”, sigma) print(“V矩阵:”, vt) df_movies = pd.read_csv(“./movies.csv”) dict_movies = {} for index, row in df_movies.iterrows(): # 获取每行的index、row dict_movies[row[“movieId”]] = “{0},{1}”.format(row[“title”], row[“genres”]) print(dict_movies) print(max(vt[1, :])) for i in range(movie_num): if (vt[1][i] > 0.1): print(i + 1, vt[1][i], dict_movies[i + 1]) |