将链表的灵活性和有序数组查找高效性 结合起来的符号表,
这就是二叉查找树,每个结点都包含两个链接(比链表中结点多一个链接),结点包含的连接可以指向NULL或者其他连接,并且只有一个父节点,(除了根节点)
基本的数据结构如下
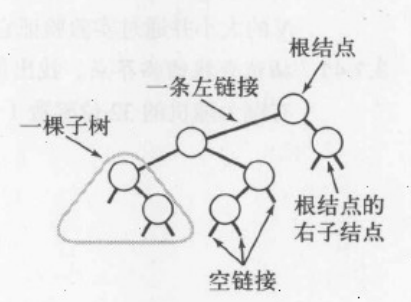
并且保证,一个二叉树中,每个结点的键都大于其左子树的任意节点且小于其右子树的任意节点.
对应的查找手段则是,如果树是空的,那么就是没有命中,如果和根节点相等,直接命中
如果较小我们就选择左边的,如果较大,我们就选择右边的
然后递归查找
同二分查找法
对二叉查找树的分析
如果完全平衡,那么空链接到根节点的距离为lgN
最坏情况,可能有N个结点
而且只要输入足够随机,插入顺序足够随机,二叉树和快速排序就是一对双胞胎
对应的插入方法,则和二分查找法融合,查找到空的位置插入,并且不停返回上一层的递归,
然后更新每一层数组数量

不断的递归往下,放入新的Node
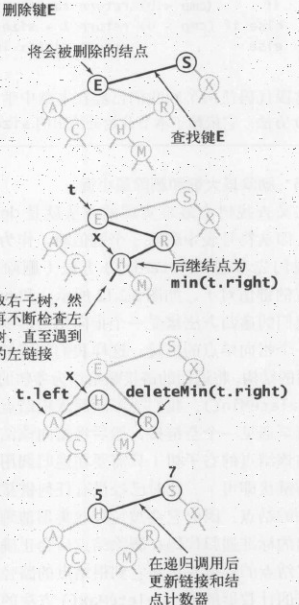
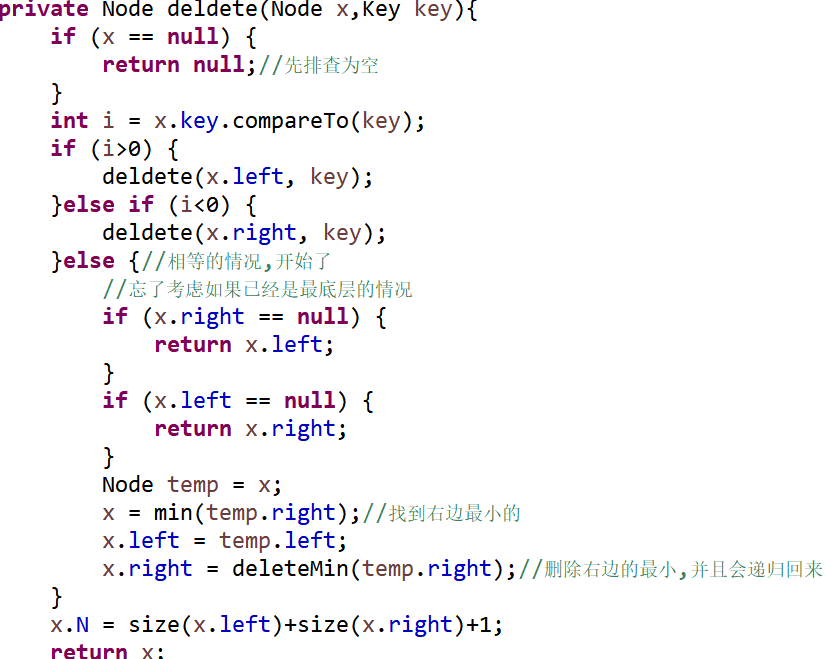
然后是删除一个键
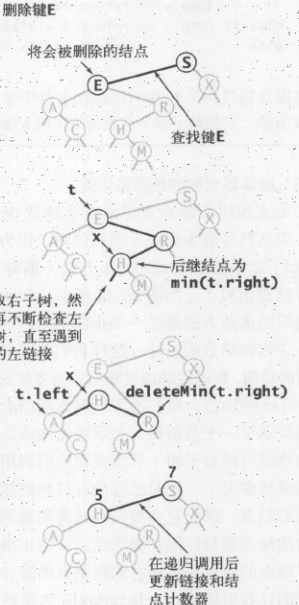
对应的删除则是如下
最后是查找的API
public Comparable[] keys() {
return keys(min(),max());
}
public Comparable[] keys(Key lo, Key hi) {
Comparable[] asKey = new Comparable[size()];//创建了一个过大的数组
keys(root, asKey,lo, hi);
return asKey;
}
public void keys(Node node,Comparable[] a,Key lo,Key hi) {
int count = 0;//设置一个辅助变量
if(node == null) {
return;//如果为空,直接返
}
int cmplo =lo.compareTo(node.key);//设置和开头比较的数
int cmphi = hi.compareTo(node.key);//设置和结尾比较的数
if (cmplo<0) {//只要比开头大,就递归向左
keys(node.left, a, lo, hi);//这一步直接递归到了最右边
}
if (cmplo<=0&&cmphi>=0) {
a[count++] = node.key;
}
if (cmphi>0) {//只要比开头小,就递归向右
keys(node.right, a, lo, hi);
}
}
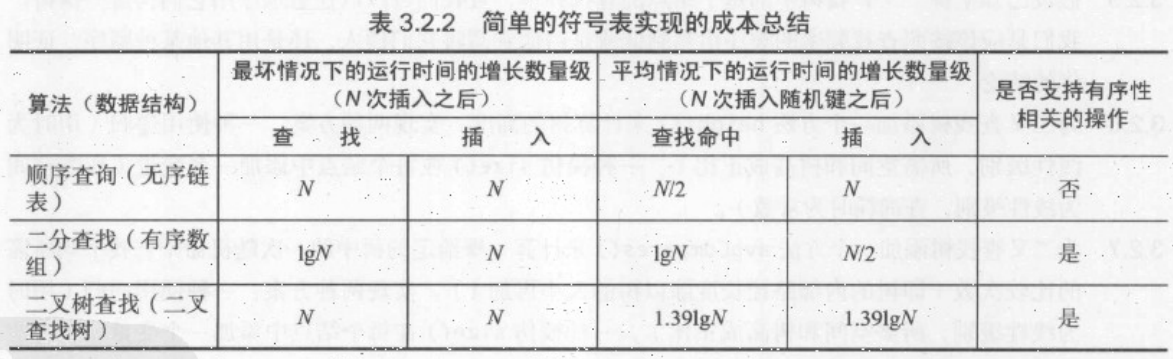
加上二叉树,我们的符号表实现如下