基础数学课27 PCA 主成分分析
我们说下一个简单的降维手段,主成分分析PCA
对于降维,我们之前说过,往往机器学习领域中,物品的特征太多。而特征太多会导致维度过多,从而加大了机器学习的难度。因此需要过滤掉一些不重要的特征。方便机器学习。
那么PCA就是一种
首先我们假设一个数据集,其中有m个样本,n个维度,整体如下
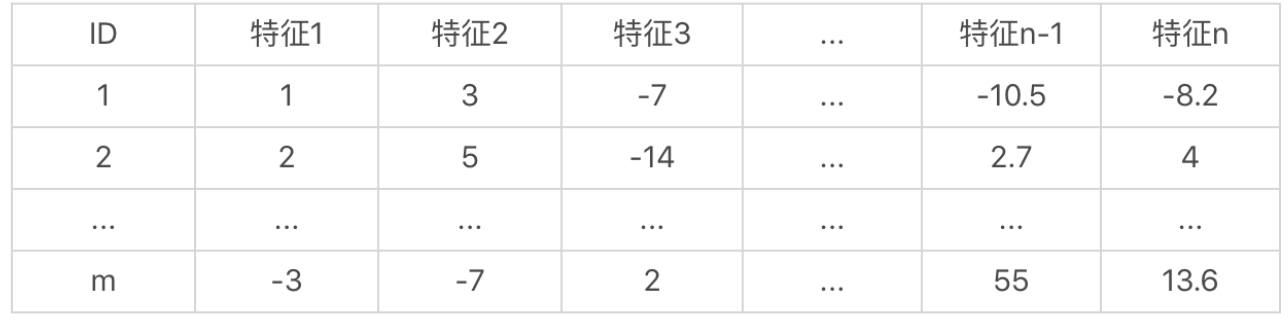
从而可以得到一个m*n的矩阵。
那么我们现在就需要降低这个矩阵的维度,保留最有用的信息。这里可以利用PCA完成,其包含了如下的步骤
- 标准化原始数据
- 获取协方差矩阵
- 计算其中的特征值和特征向量
- 挑选主要的特征向量
- 生成新的特征
对应步骤我们分开讲解下
- 标准化
这里我们利用特征标准化,进行处理
Y = (x-u)/(q)
其中x是原始值,u是均值,q是标准差(方差)
Y是变化后的值,这样我们就可以将同一维度的数据进行标准化。
这里我们假设有一个样本集合,包含了三个样本,每个样本具有3个维度特征
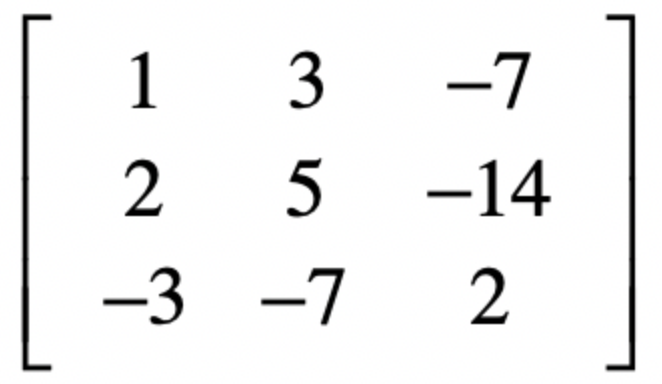
这里我们进行标准化
第一维度的数据就是 1 2 -3 平均值0,方差为
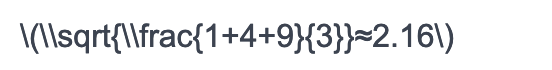
之后我们可以套入前面的公式
得到第一维度的数据,1/2.16=0.463,2/2.16=0.926,-3⁄2.16=-1.389
最终得到的标准化矩阵为
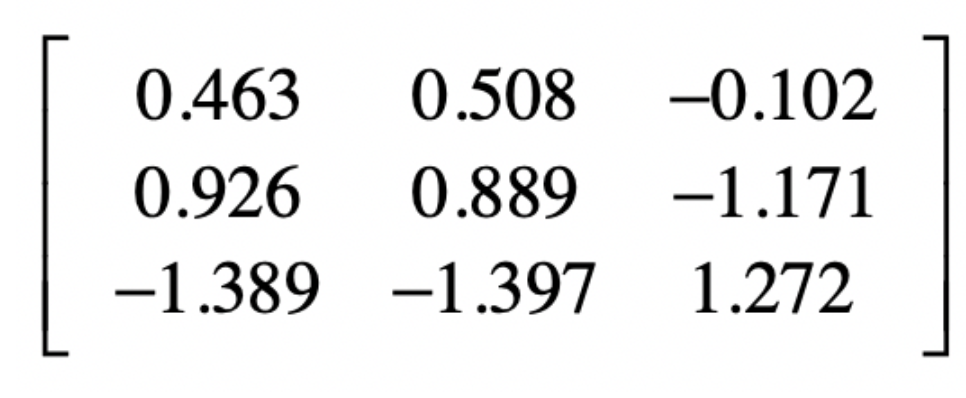
- 获取协方差矩阵
协方差用于衡量两个变量之间的总体误差。假设两个变量为x y
采样数量为m,计算公式如下
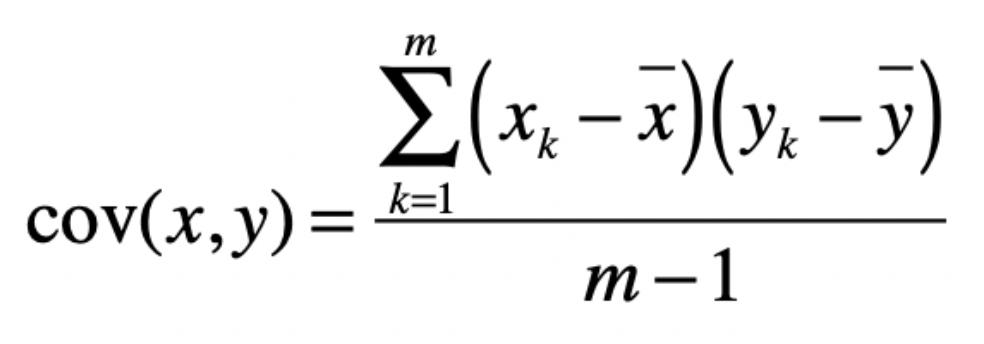
其中xk为X维度的第k个数据
减去了X维度的平均值。
将Xk转换为维度中的值,可以为Xki
其中k为行,i为列,转换公式为
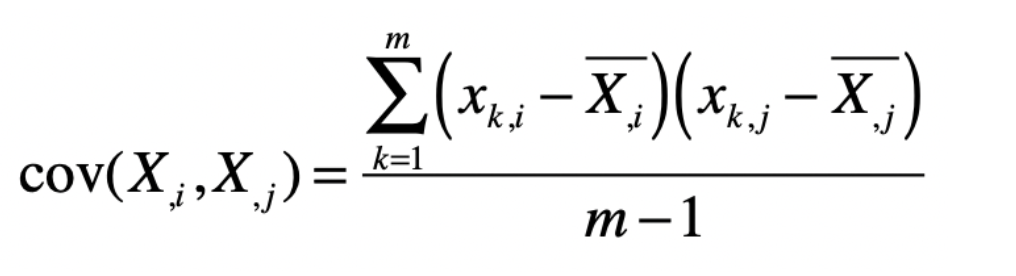
再之后,协方差矩阵就会变为如下形式
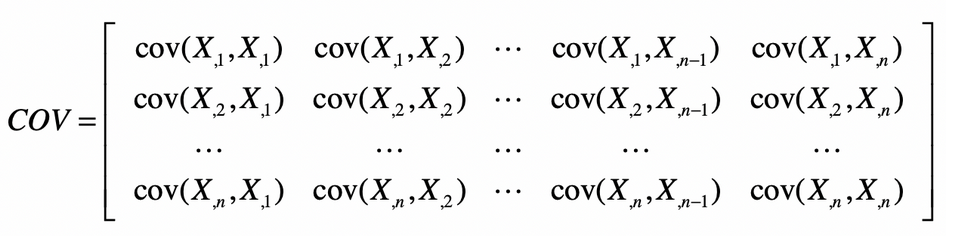
并且由于 cov(X2,X1)和cov(X1,X2)具有对称性,所以cov是一个对称矩阵,在主对角线上的值就是各维特征的方差。
对于上面得到的矩阵,我们就可以计算其协方差矩阵
第一维度的方差为
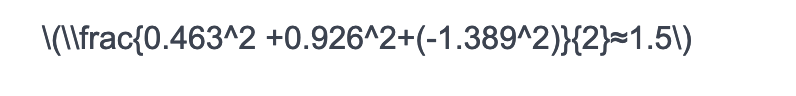
第一维度和第二维度的协方差为

得到了协方差矩阵
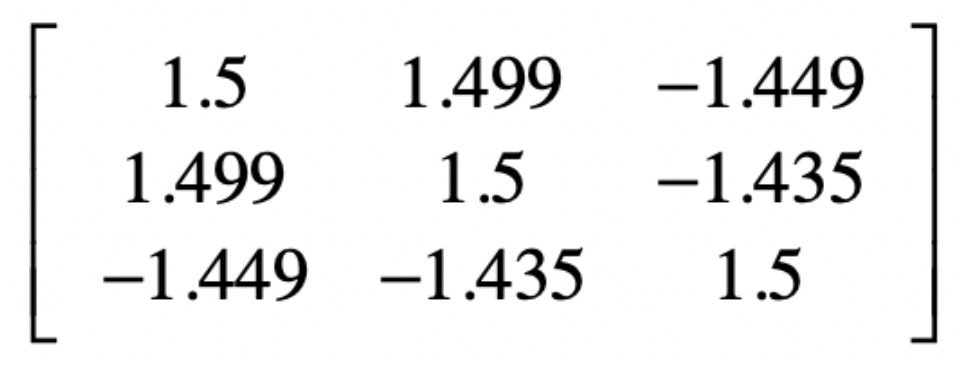
之后我们就可以解协方差矩阵的特征值和特征想来那个
- 计算协方差矩阵的特征值和特征向量
这里的特征向量和我们说过的机器学习中的特征向量并不是一回事,但是在这里我们先给一个计算公式。
Xv=λv
其中v是X的特征向量,λ是对应X的特征值,所以
(X−λI)v=0
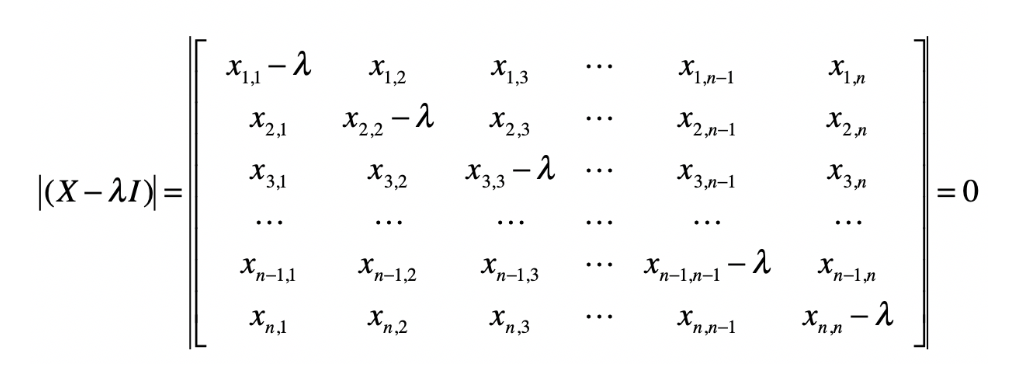
并计算行列式
(x1,1−λ)(x2,2−λ)…(xn,n−λ)+x1,2x2,3…xn−1,nxn,1+…)−(xn,1xn−1,2…x2,n−1x1,n)=0
通过这个方程式,得到多个解,并计算特征值。
将上述的协方差矩阵带入上述公式得到
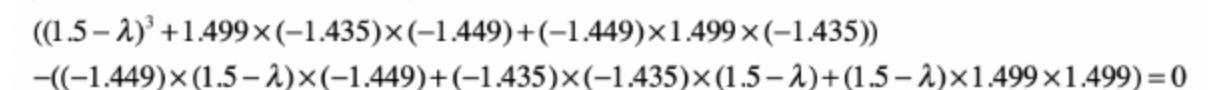
得到
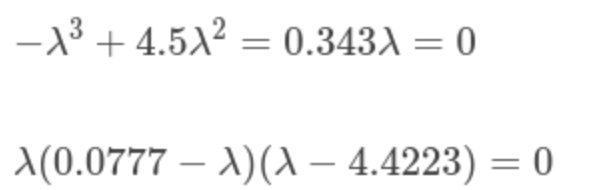
于是其具有三个近似解,分别为0,0.0777和4.4223
将这三个特征值带入原方程,得到特征向量
这里补充下如何通过特征值得到特征向量
比如0.0777,这里可以带入上面的矩阵
[1.5 – 0.777, 1.499,-1.499]
[1.499, 1.5 – 0.777,-1.435]
[-1.499, -1.435,1.5 – 0.777]
左乘一个
[x1]
[x2]
[x3]
令其为
[0]
[0]
[0]
得到方程,其中包含x1 x2 x3的变量,最终得到特征向量。
这里我们根据4.4223得到对应的特征向量为
[-0.58077228 -0.57896098 0.57228292]
最后根据多个特征值以及其特征向量
通过排序,获取到重要的特征向量。
利用前k1个特征向量,组成一个n*k1维度的矩阵D
然后将原始的m*n维度矩阵乘以矩阵D,得到一个m*k1维度的矩阵,从而进行降维操作。
这里我们利用特征值和特征向量对原样本矩阵进行变化

这样就进行了特征维度的降维操作。
那么最后,我们说下协方差矩阵的核心思想
降低维度,就是要筛选出去那些表达信息少的维度,保留具有较高识别的维度。
那么如何判断维度的信息量包含大小,可以从两方面,一方面可以查看这个信息维度内的差异是否大,如果包含的信息量差异大,就可以认为更加具有辨识度。
另一方面则是查看维度之间的关联性,如果是如果两个维度具有很高的相关性,那么表达的信息就是重复的。
这里可以使用皮尔森系数来进行计算。
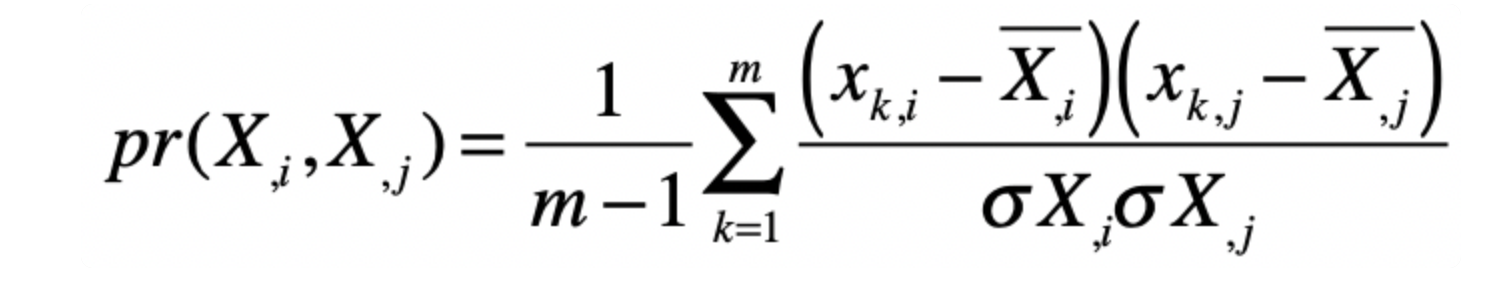
其基本上和协方差类似。
利用协方差来衡量不同维度的相关性。
最终在协方差矩阵中,对角线的是维度自身的信息量大小,其他的为不同维度之间的相关性。
之后就可以计算得到特征值和特征向量,对于这个协方差矩阵,我们需要考虑尽可能的保留大信息量的维度,去除其他的不相干维度。
也就是对协方差进行对角化,然后使得矩阵只有主对角线上有非0的元素。
那么特征值和特征向量,就是为了方便变化上面的矩阵,让矩阵在一个新方向进行变化,从而尽可能的保留原有的信息,而新的方向上,包含多个原始特征的组合和缩放。