Heaven.Blog

基础数学课27-1 奇异值分解

另一种降维的方法，SVD奇异分解，和PCA不同的是，SVD尝试通过样本本身的分解，找到潜在原因，从而实现降维。

使用SVD的时候，核心概念是矩阵分解。

矩阵分解中包含两个概念，分别是方阵和酉矩阵

方阵是一种特殊矩阵，行数和列数相等。一个矩阵的行和列如果都是n，那么可以叫做n阶矩阵。

如果一个矩阵和转置矩阵相乘得到的是单位矩阵，就可以叫做酉矩阵。

X’X=I

而上一节，我们学习了特征值和特征矩阵，我们可以将X进行特征分解，获取到矩阵X中的k个特征值λ1，λ2，…，λn，以及对应的特征向量v1，v2，vn

且XV=VΣ

其中V是n个特征向量的n阶矩阵。Σ则是表示n个特征值为主对角线的n阶矩阵

XVV−1=VΣV−1

XI=VΣV−1

X=VΣV−1

这里第二步骤需要注意，X乘以一个单元矩阵，得到的还是自身。

这里进行一下验证上面最后一步得到的公式

那么证明的公式如下

接下来就是矩阵的奇异值分解了

如果矩阵X是一个m*n的矩阵，那么其SVD为X=UΣV’

SVD不要求分解的矩阵为方阵，所以U和V’并不是互为逆矩阵，其中U是m*m

V是n*n维的矩阵。Σ 是一个 m×n 维的矩阵，但是其只有主对角线上的元素非0.也就是一个单位矩阵。

对于这三个方程，’我们获取方式如下

首先是，X虽然不是一个标准的方针，但是我们将X进行转置X’

针对X’X进行特征分解，得到特征值和特征向量(XX’)vi​=λi​vi​

因此得到了n个特征值和n个特征向量v，因此可以构造一个n*n维度的矩阵V，称为右奇异变量。

同样对XX’进行特征的分解，得到的特征向量构造一个m*m的矩阵X，为U矩阵。

最后是奇异值矩阵Σ了。其需要确保对角线的值是奇异值，其他的填充0.所以可以得到

X=UΣV’

XV=UΣV’V

XV=UΣI

XV=UΣ

Xvi​=σi​ui​

σi​=ui​Xvi​​

通过计算得到多个奇异值，最终得到奇异值矩阵。

那么这样的一个SVD矩阵有什么用呢？

比如我们之前说的词条矩阵，首先构造字典，利用字典构造每篇文档的向量，然后通过文档的向量构造矩阵，矩阵的列和行表示文档和词条。最后从而实现利用距离或余弦夹角来进行匹配。

上述的唯一缺点是需要进行精确匹配，没法获取到同义词的匹配情况

而LSA 潜在语义分析利用SVD解决了。

其中包含了一些步骤

1. 分析文档集合，建立文档和词条矩阵
2. 对矩阵进行SVD分解，利用奇异值得到语义模糊概念，也就是学校-学生-老师都是教育这个概念的
3. 得到V U 其中V矩阵表示词条和语义概念的关系强弱，U表示文档和语义概念的关系强弱。

最终形成如下图，也就是语条-语义-文档的关系

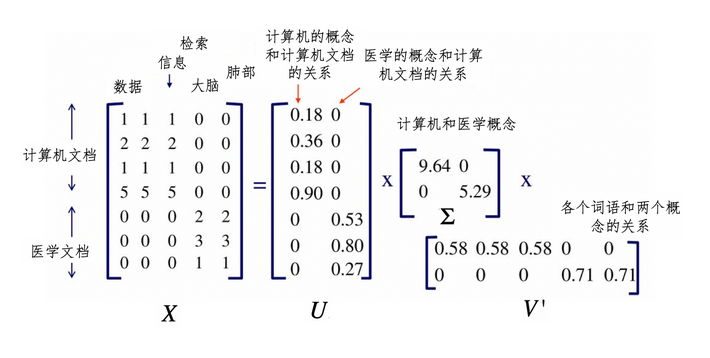
利用U查找哪些文档和不同领域有关

利用V表示单词和概念的关系，这个单词属于哪个概念。

1. 进行降维，降维的操作和pca类似。
2. 重新构建概念-文档矩阵，其中元素不再表示词条，而是概念。

总结一下，我们说了SVD奇异值分析，提供了一种可行的方案，运用了矩阵X和自己的转置生成对称方针，以及不同的矩阵U和V，最终得到奇异值矩阵。

从而利用最终的奇异值矩阵进行降维。