线性代数的总结
之前，我们说了PCA，说了SVD，那么在SVD之中X’X的特征向量可以构成V矩阵， X X’的特征向量组成U矩阵。这样的操作是怎么做到的呢？
首先是矩阵乘法的几何意义
在讲解PCA主成分析的时候，说了协方差矩阵转换的主要变量是特征值和特征向量。而特征向量主要就是表示了矩阵在空间中的变换方向，这些方向是正交或者近似正交的。特征值则是在方向上伸缩的比例。
对于正交，之前说过，如果两个向量的点乘结果是0，那么其就是正交的。在酉矩阵之中，矩阵和矩阵转置相乘为单位矩阵，那么在这个矩阵中就是正交的。
这里我们给一个空间投影
比如我们定义一个二维空间，其横坐标为x，纵坐标为y，给定一个点（1，2），画出如下图。
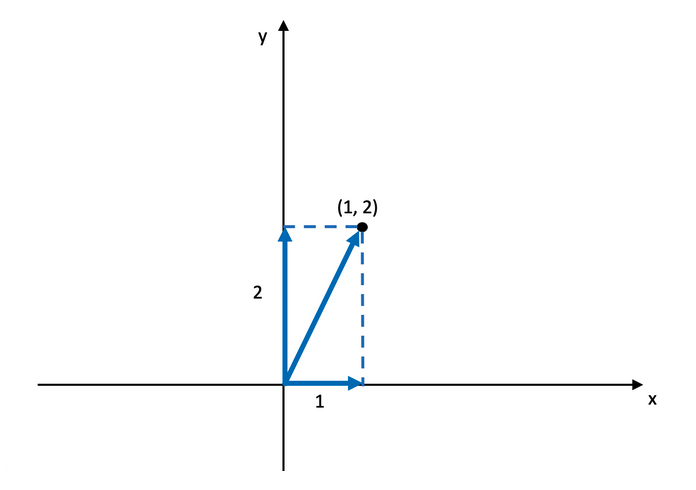
此时我们给予一个矩阵X1来进行左乘
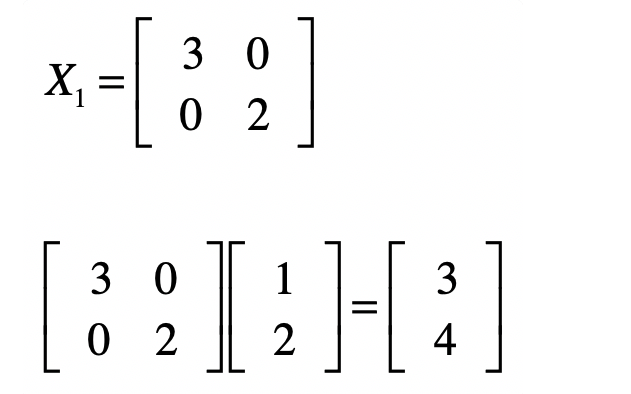
这类似一种降维的操作。
这样我们将其体现在图中
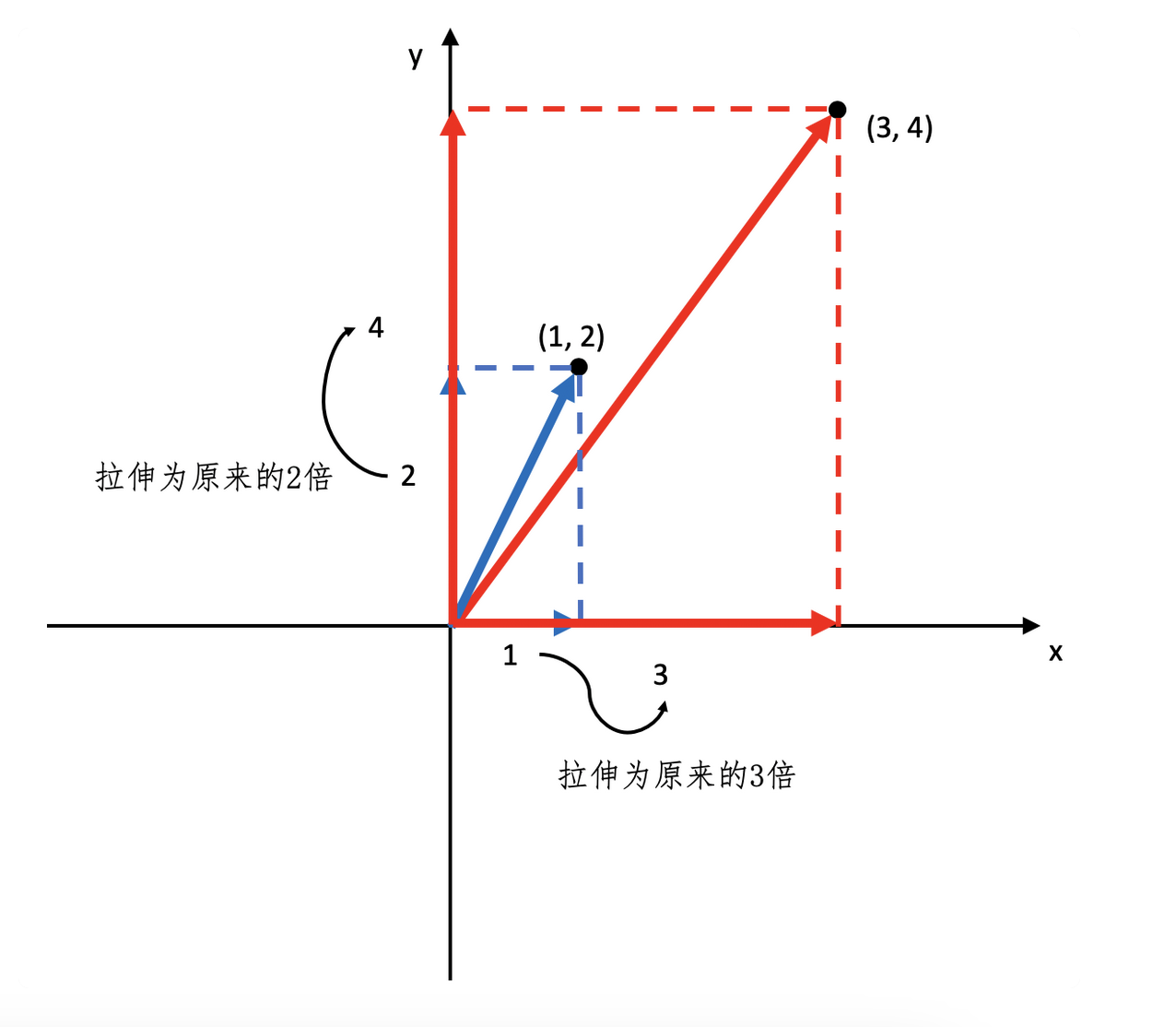
对于这个图的变化，我们可以如下理解
首先X是一个对角矩阵，也就是只有对角线上值非0，这个对角矩阵的特征值为3和2
对应的特征向量为 [1,0] 和 [0,1]
在二维坐标中 1，0表示x轴方向
0，1则是y轴方向
特征值为3是在x轴上拉伸为3倍，特征值2表示y轴上拉伸两倍，如上图所示。
如果特征向量不是一个简单的x轴和y轴上的，可以是二维空间中任何正相交的向量。比如
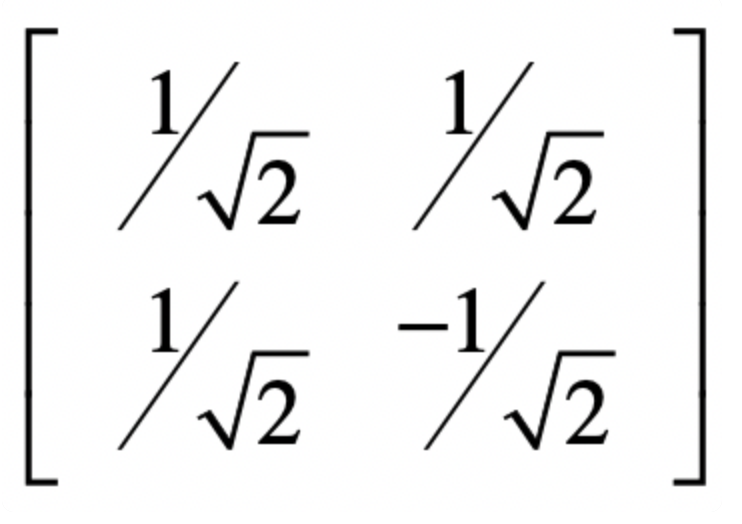
给予了一个正交的矩阵，这个矩阵还是一个酉矩阵，这个酉矩阵可以形成对角矩阵，也就是VV’=I 这里我们给予假设的特征值矩阵，我们就可以构建一个用于测试的实际矩阵X2.，这里采用的函数为 X2 =VΣV’
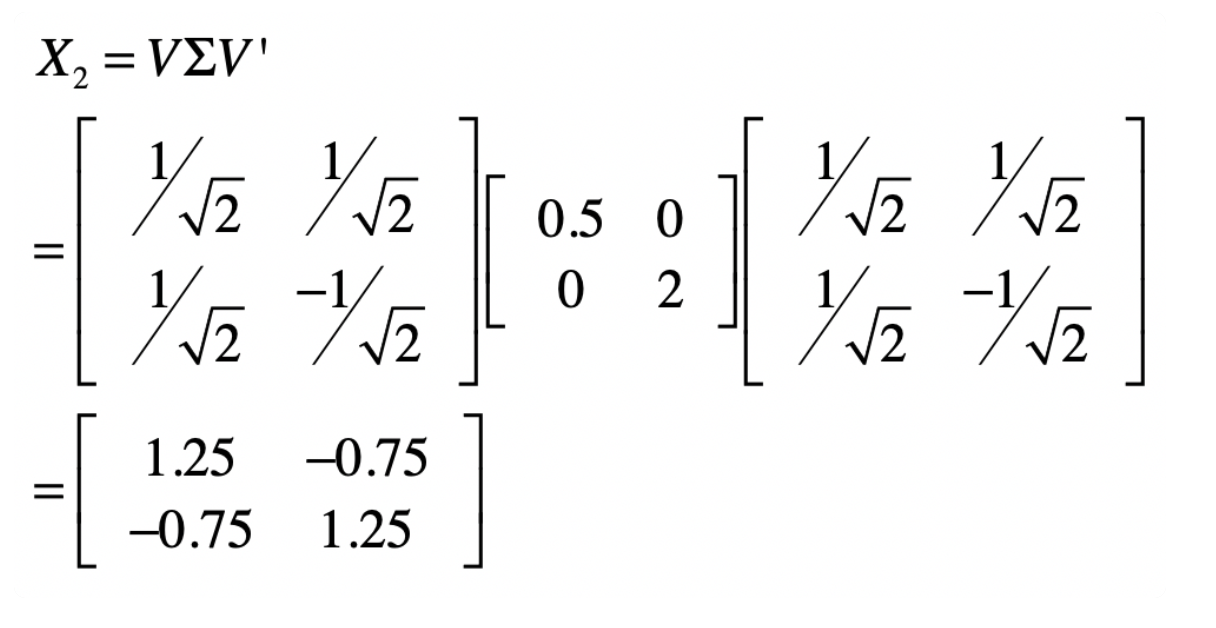
这里我们还可以顺手验证X2 左乘一个向量，就是沿着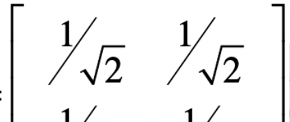 
方向压缩一半, 在 
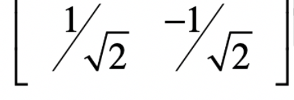方向增加两倍。
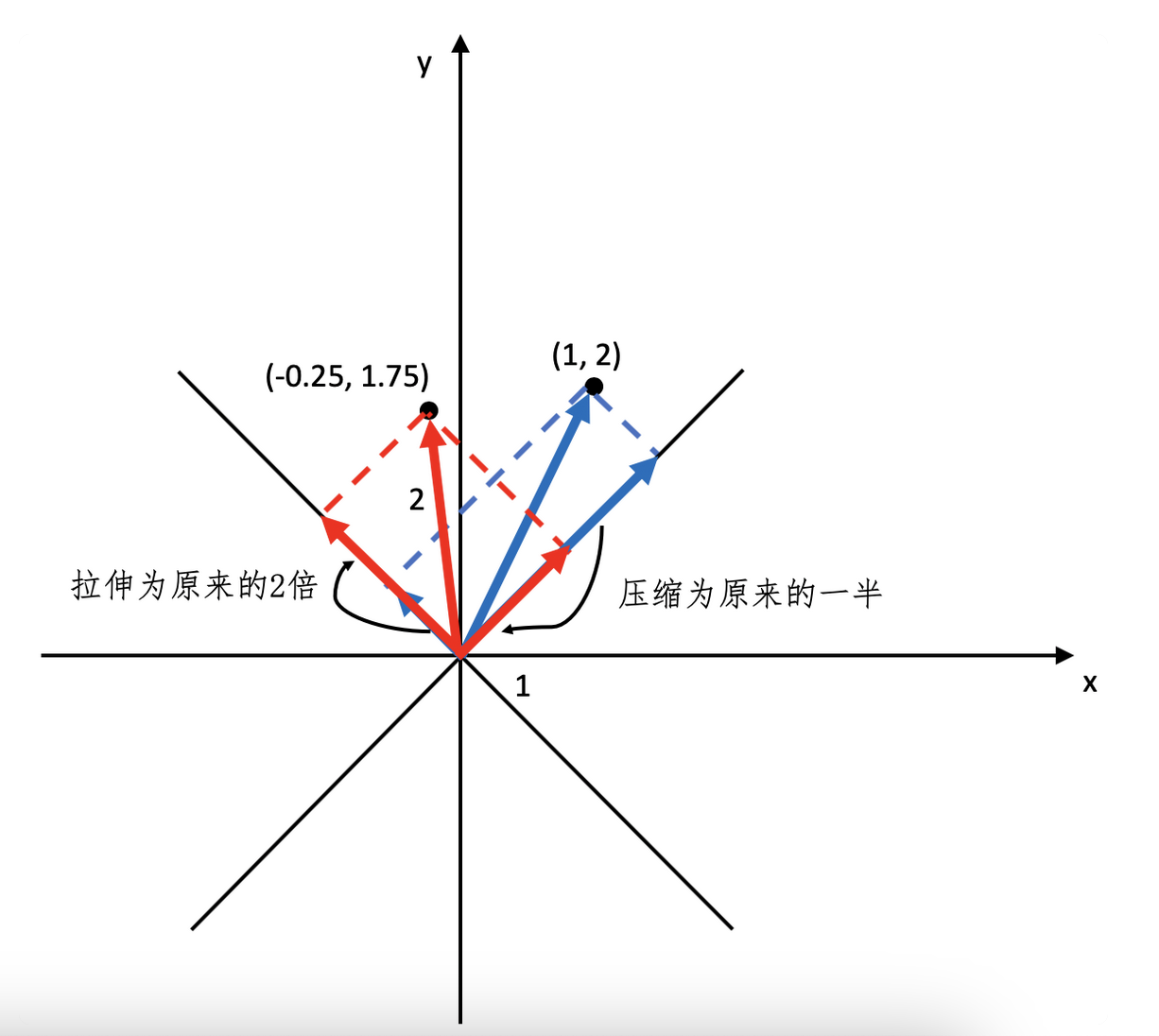
比如我们在X2上左乘（1，2），得到新向量
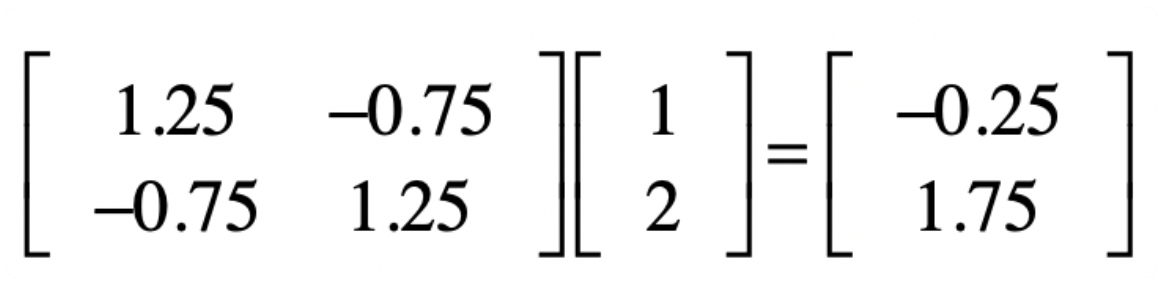
那么我们将原本的-0.25，1.75和1，2两个坐标放在二维坐标系上，分别和原本的
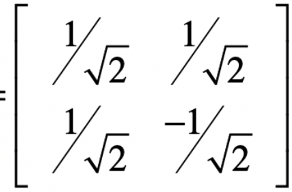方向上投影。
从而进行对比
那么在了解了矩阵左乘向量的几何意义，矩阵左乘矩阵就类似了。
假设X矩阵左乘Y矩阵。将Y矩阵看作一系列列向量的集合，
让X矩阵针对Y中的列向量进行变化。
之后还有SVD中的U和V矩阵
如何说明X’X形成V矩阵，XX’形成U矩阵
首先是V矩阵的证明
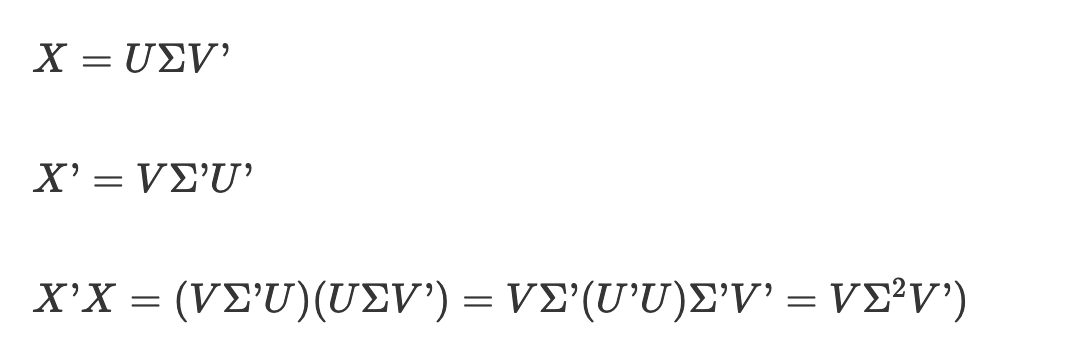
U是酉矩阵，所以U’U=I 所以可以被省掉。
然后Σ’Σ=Σ2 所以Σ2 仍然是对角矩阵。所以X’X=VΣ2V’中V的向量为X’X 的特征向量。特征值为Σ2对角线上的值。
同理，可以得到U为XX‘的特征向量。
那么我们总结下线性代数，其包含了向量，矩阵以及对应的操作
向量表示了一组数的概念，表示一个对象的多维特征。从而广泛的运用到信息检索和机器学习的领域中，其中还包含了多维特征。矩阵包含了多个向量，适合表示多个数据对象的集合。利用这两者的特性，我们可以将其运用到多种算法和模型中。比如查找相似程度，归属关系等。
还可以用于发现不同维度特征间的关系。进行特征降维。