基础数学课26 矩阵
我们看下矩阵的相关计算,矩阵由多个长度相等的向量组成,每列或者每行都是一个向量。我们将向量看作一维数组,矩阵就是一个二维向量数组。
利用二维矩阵的特性,矩阵就可以表达二元关系了,这里我们就从图的邻接矩阵开始出发,展示如何使用矩阵计算来实现PageRank算法。
这里我们回顾下PageRank算法,其模拟了一个随机冲浪者的模型,从某个网页开始出发,根据Web页面中的链接关系进行随机访问。从而不断的访问下去,只不过在此基础上,PageRank还加入了跳出的逻辑。
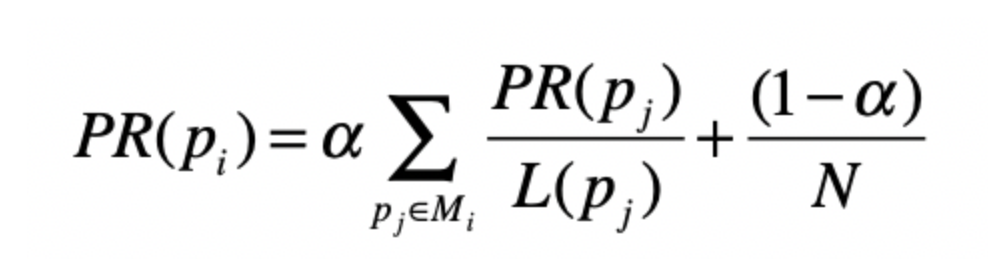
其中Pi 或者Pj表示第i或第j个网页
Mi是第i张网页入链接集合
PR(Pj)子的是Pj的PageRank的得分
L(Pj)表示Pj的出链接数量。
那么这就表示了从Pj调到Pi的概率
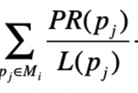
后面的a和N代表着,N为网页的数量 a为不跳转的概率。
PageRank是迭代法实现的,一开始所有的网页节点PageRank设置为相同的数。
然后得到每个节点的新PageRank值,当一个网页的PageRank发生了变化,会导致相连的所有页面都会发生变化。因此可以使用这个公式,进行迭代式的修复。
最终在多伦迭代后,得到一个稳定的值。
那么这个如何和PageRank扯上关系呢?
如果我们先把跳出的概率隐藏掉,那么这个公式就变为了
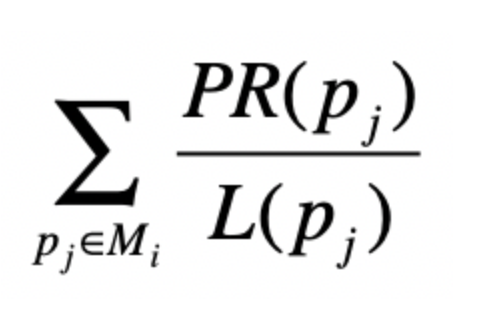
这时候再引入矩阵的点乘公式
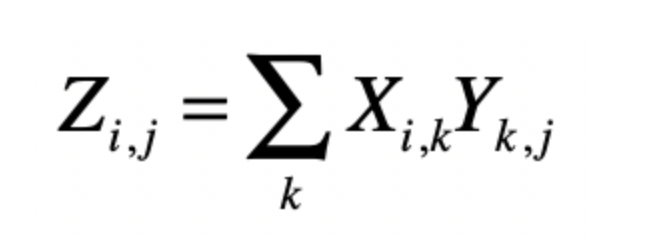
这时候就可以将PageRank的计算,转换为两个矩阵的点乘,一个矩阵式每个页面的PageRank,另一个矩阵为接邻矩阵,其表示图结点的相邻关系的矩阵。
我们假设一开始的PageRank为1
那么主要就是接邻矩阵,对于这个矩阵中的元素,第i行第j列的元素,我们可以使用其表示页面pi到页面pj的链接,如果存在链接就是1,不然就是0.
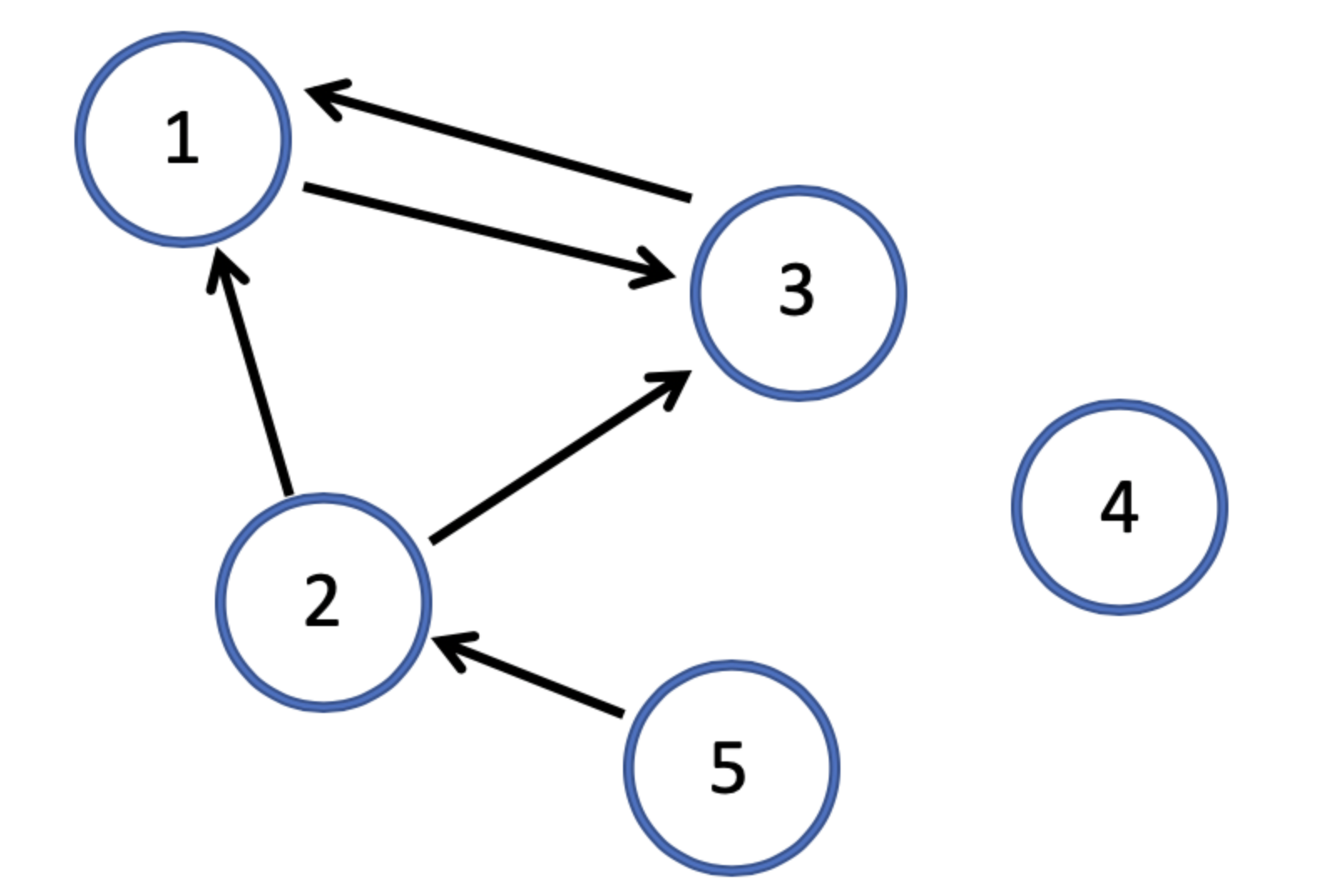
这个图的邻接矩阵为
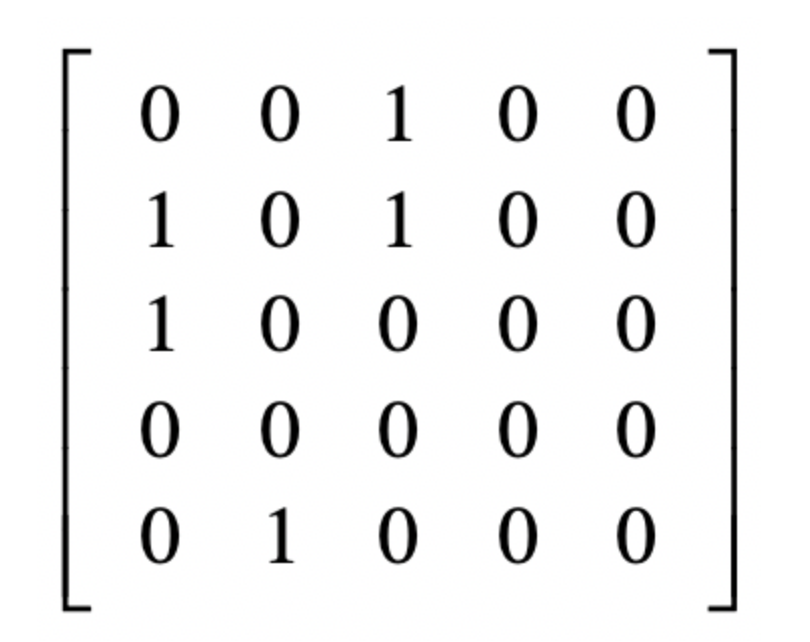
然后我们进行一个归一化处理,矩阵为
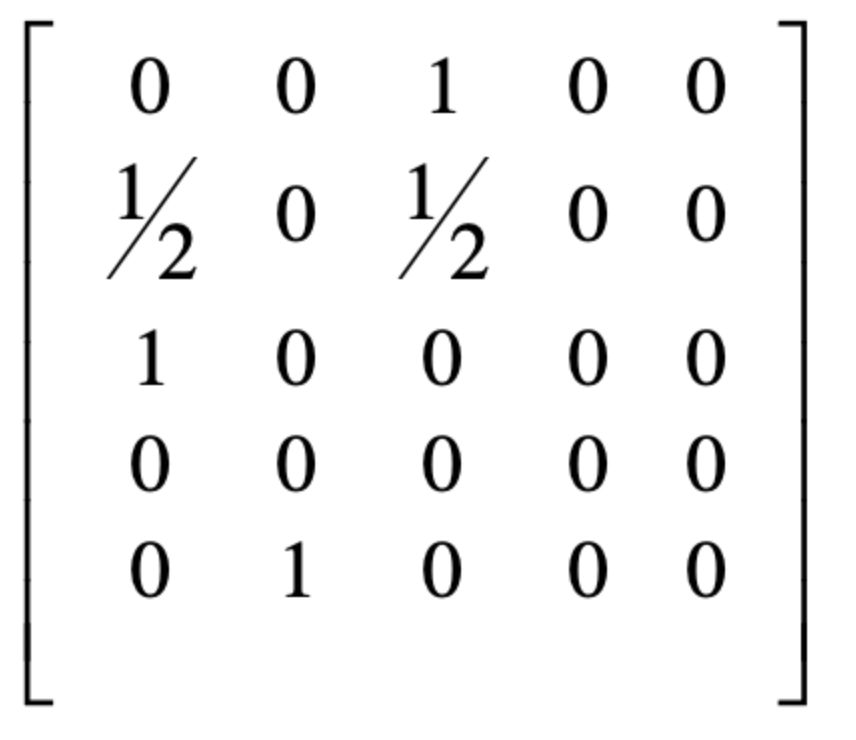
这里我们就可以进行一个PageRank的处理,第一次迭代操作为
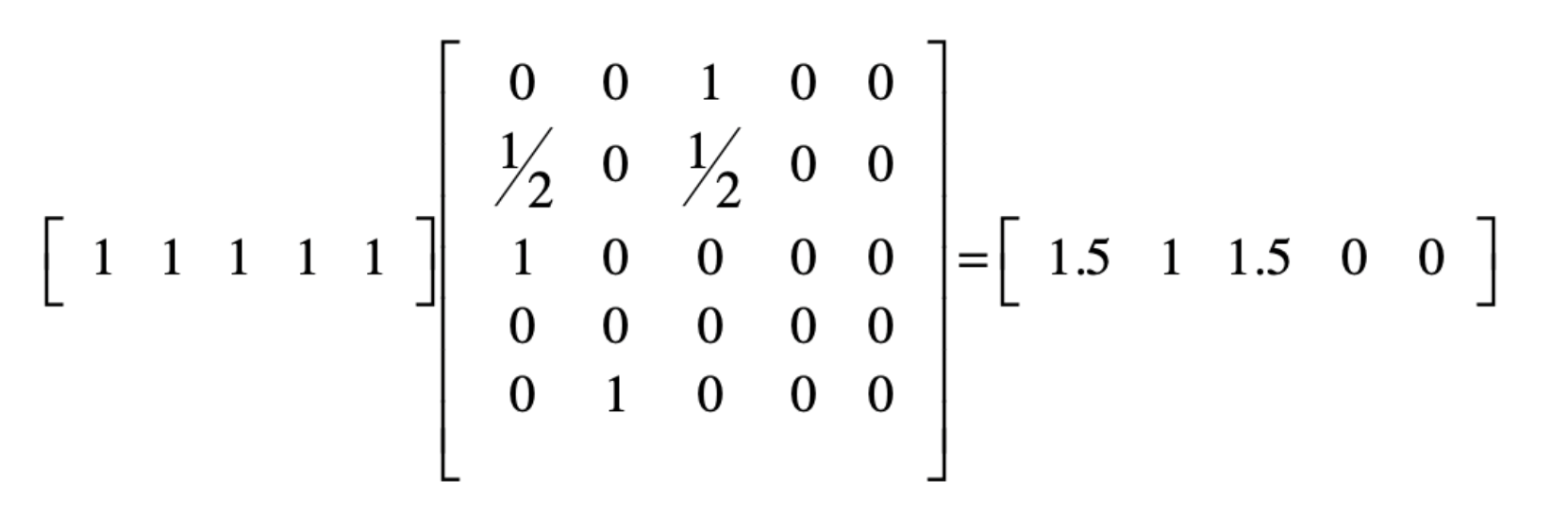
如果考虑随机跳转的话,我们就需要在每次迭代之中,在进行一次点乘。
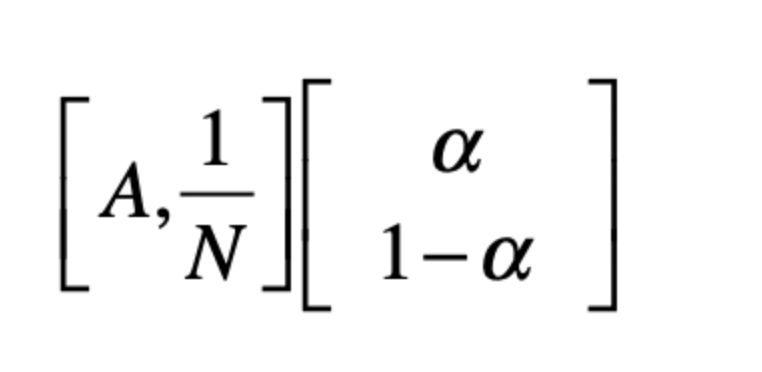
也就是
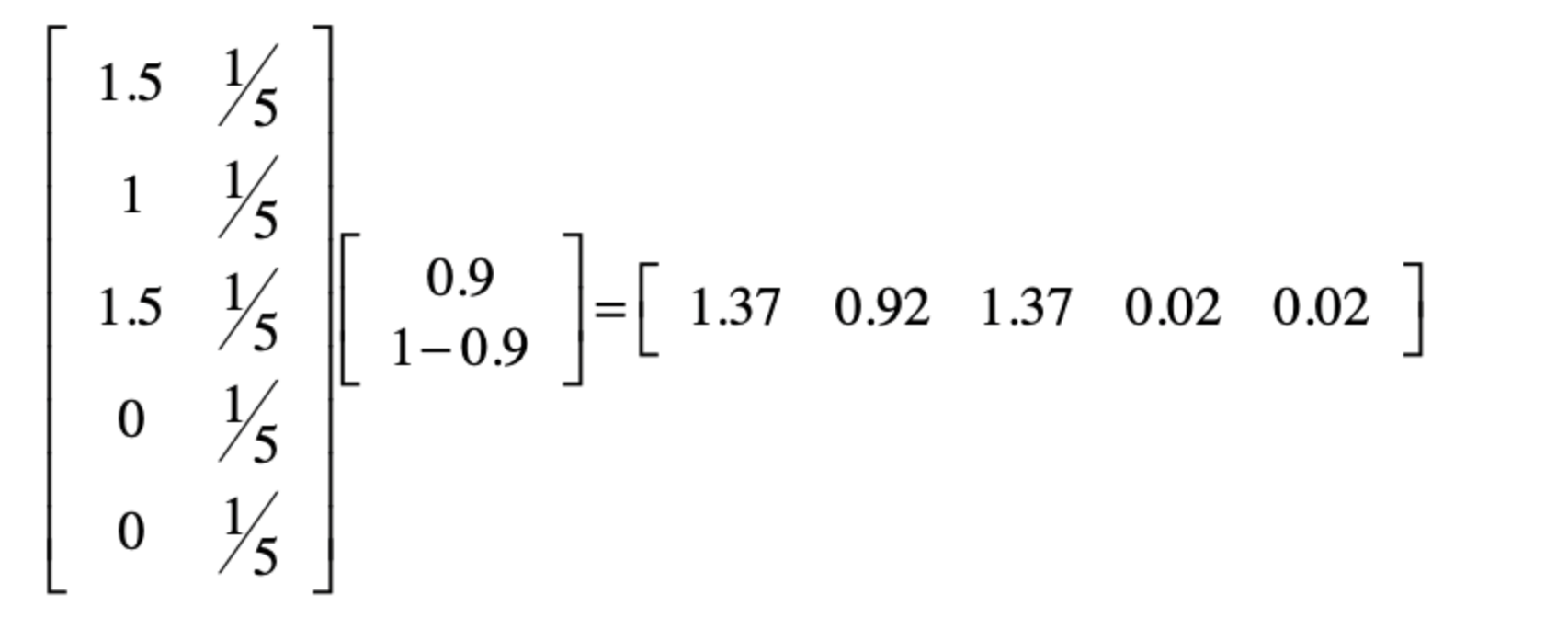
最后得到结果集,还可以在每一轮中进行归一化处理

对应到Python代码中,可以使用如下代码实现。

然后使用迭代计算PageRank,不过这里我们设置一个迭代上限

最终获取得分。
这里我们使用PageRank计算了矩阵得分,这种情况下,矩阵点乘体现了马尔科夫过程中的状态转移。
除了PageRank之外,我们还可以使用矩阵操作来进行协同过滤推荐,其中利用用户和物品之间的已知关系,来为用户提供新的推荐内容。
我们这里就说下如何实现协同过滤推荐算法,不过在此之前,我们先说下这个算法的核心思想。
简单来说,就是根据当前用户的喜好,来推荐其他可能感兴趣的商品。推荐的来源在于,需要先找到当前和当前用户具有相同或类似品味的用户,然后根据其他用户的选择,给这个用户推荐新的商品。
更加详细的,在推荐算法中,我们可以利用矩阵表示这种二元关系,

其中Xij 表示的第i个用户对j个物品的喜好程度,这里的喜好程度可以由用户的购买次数或者打分决定。
再有了这样一个用户矩阵之后,我们就可以一方面计算用户之间的相似性,一方面对喜好进行预测。
对应的的公式就如下,假设有m个用户,n个物品,就可以使用m*n的矩阵来表示对物品喜好的二元关系。
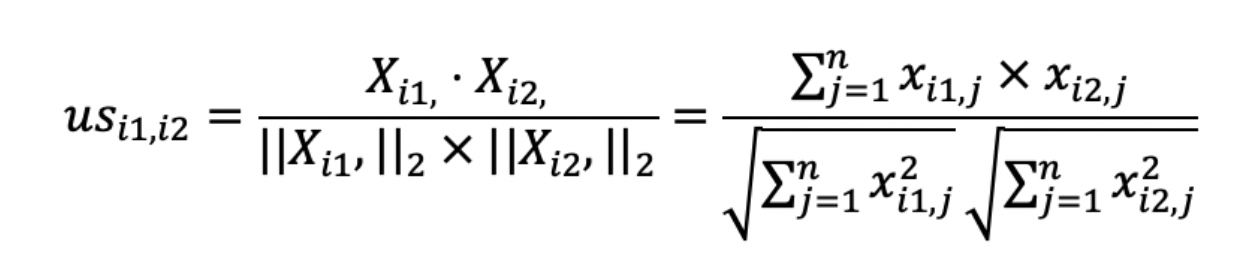
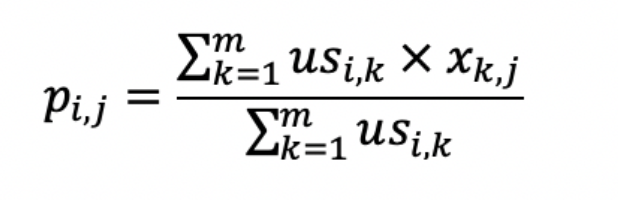
第一个公式是用来计算用户之间的相似度
X i1 表示第i1行的行向量,也就是用户的喜好向量
Xi2 表示i2行的行向量,也是i2用户的喜好向量。
分子是点乘,分母是乘积。
第二个公式利用第一个公式的用户相似度,以及对物品的喜好,预测用户对其他物品的喜好程度。
其中usi,k 表示用户i和k之间的相似程度, xk,j 表示用户k对物品j的喜好程度。同时除以 usi,k。 进行归一化处理。
对于第二个公式来说,如果越相似,那么得到的结果必然越大。从而实现了相似用户的推荐。
对于公式,这里我们通过一个假数据集来看下
我们已经有了一个喜好度矩阵X

这样我们需要获取到用户的喜好向量,这里可以通过点乘的方式来实现,也就是XX‘

这时候就可以计算us的值了,如果us1,2

而us代表的是用户之间的相似度,通过us,我们计算任意用户对任意商品的喜好程度。

得到了第二个公式中的分子,而分母可以为分子中US的按行求和。

利用USP和USR相除,得到结果为

那么我们就知道了任意用户对任意商品的喜好矩阵。
就比如第一个用户对第三个商品的喜好度,理论上大于0,而之前用户从没接触过,这就可以进行推荐。将物品3推荐给用户1.
除此外,对于这个商品的推荐算法,我们往往还需要考虑到,有的用户比较严苛,有的用户比较宽松,高分比低分更常见。所以我们需要进行归一化以及标准化处理,最后进行协同过滤。
除此外,我们还可以利用物品之间的相似度进行计算,同样得到用户对物品的喜好程度。
那么总结一下,我们说了下协同过滤算法如何通过矩阵求得。并说明其核心思想是先计算用户或物品的相似度,并最后推测出推荐结果。