基础数学课8-树的深度和广度优先遍历
首先,我们需要明确基础概念,即什么是树
树是一种简单的,没有回路的连通图。如果一个图里的边具有方向,即为有向图,如果边没有方向,则是无向图。
最简单的树的实例即单词树,可以让用户不断遍历树上的节点,让从而找到树上是否包含想要查找的单词。
那么我们对于单词树来说,我们如何想要编程实现一个这样的结构,就需要实现两类操作,也即构建前缀树和查询前缀树。
构建前缀树需要将单词拆分为字符,然后根据字符的前后遍历,判断树上是否存在对应的节点,当节点不存在的时候,就需要在上一个字符的节点下增加一个子节点。直到所有的字符都加入到了树中。
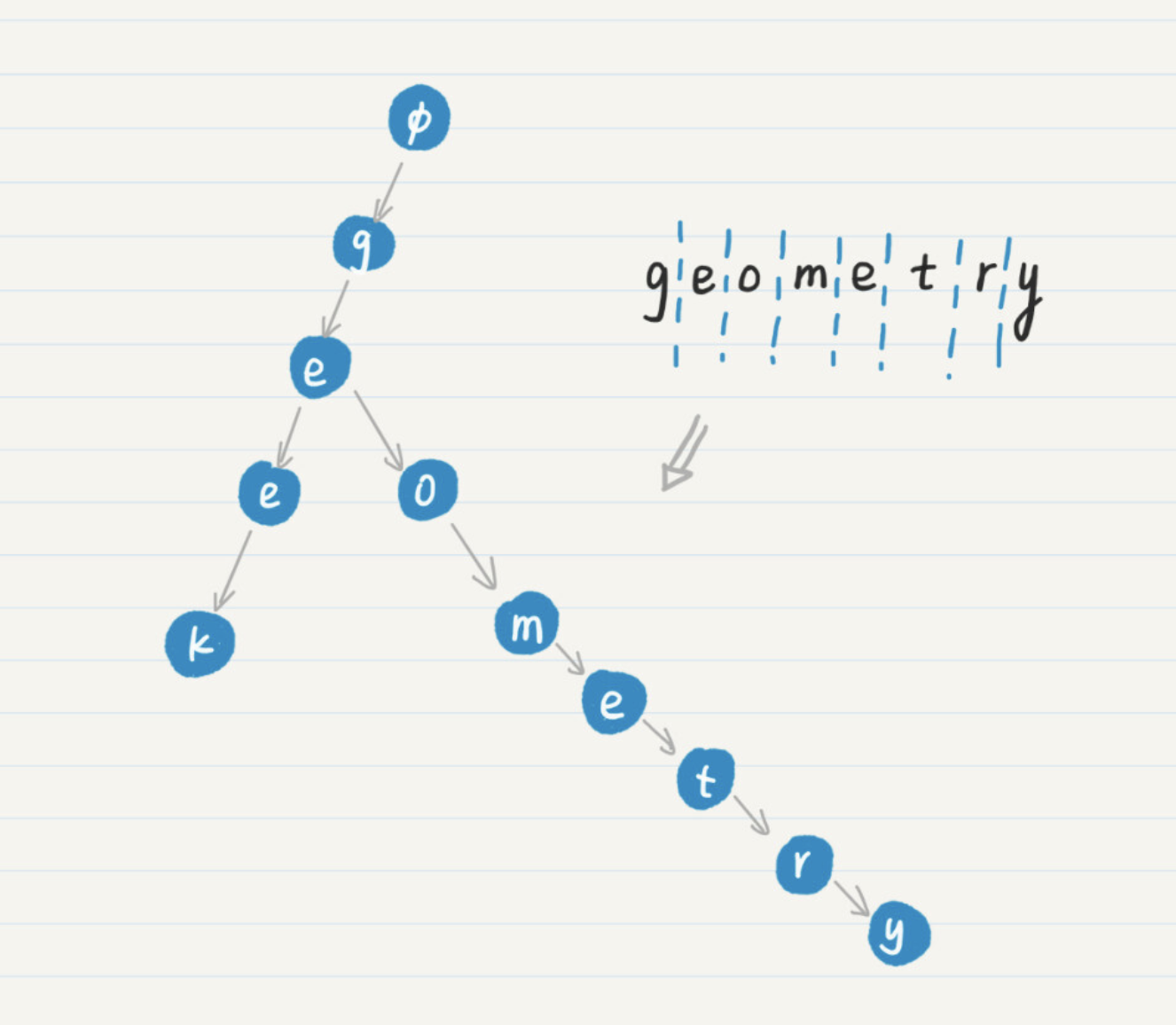
查询前缀树则是在树上遍历。不断判断字符在树上存在。当单词所有的字符都存在于树上的时候,判断最后一位字符在树上的节点是否标记自己是一个单词的末尾了,如果符合条件则认为找到。
同样,如果走到了树的叶子节点或者没有匹配到字符的节点,则认为查找失败了。
其实本质上,构建和查询都是在遍历树。那么我们将遍历树的方式区分为了深度查询和广度查询。深度遍历类似于递归查询,就是从树的根节点出发,然后沿着这个边向下查询,然后不断的递归向下查询,当没法递归或不符合条件了则递归兄弟节点。通过不断的重复,直到查找到目标的节点。
对应到我们查询单词,就是当查询当前节点不符合的时候,直接返回。
那么我们该如何用代码的方式实现深度优先搜索。
首先是利用数据结构来明确树的节点。这里我们采用链表这种数据结构实现树,方便实现树的多重入度和多重出度。
这里我们设计一个TreeNode类,表示树的结点和边。
其中节点的label属性代表了哪个字符串
其次是节点具有哪些子节点
最后还需要一个标志位,来表示是不是单词最后一位。
| /**
* @Description: 前缀树的结点 * */ public class TreeNode { public char label; // 结点的名称,在前缀树里是单个字母 public HashMap<Character, TreeNode> sons = null; // 使用哈希映射存放子结点。哈希便于确认是否已经添加过某个字母对应的结点。 public String prefix = null; // 从树的根到当前结点这条通路上,全部字母所组成的前缀。例如通路b->o->y,对于字母o结点而言,前缀是b;对于字母y结点而言,前缀是bo public String explanation = null; // 词条的解释 // 初始化结点 public TreeNode(char l, String pre, String exp) { label = l; prefix = pre; explanation = exp; sons = new HashMap<>(); } } |
在之后我们通过递归来实现深度优先搜索。
不过在实现过程中,我们需要注意的,搜索的时候的临界情况
并在最后,利用递归下钻,实现深度递归。
其次是广度递归。对于广度递归来说,我们可以利用人脉问题来进行计算
在社交软件中,如果我有一个好友,我的好友拥有的好友其实可以算作位我的潜在好友。那么如果我多个好友都有一个共同潜在好友,那么APP就可以考虑将这个共同的潜在好友推荐给我。
所以我们需要拿到用户所有的好友及好友所有的好友,最后取出来所有的树中长度为2的好友列表,进行返回。
如果这样的一个需求,如果我们直接使用深度搜索,那么需要按人头进行搜索,也即为搜索一个人的所有2度好友后,然后再获取下一个人,那么效率太低了。
所以我们引入了广度搜索,也就是先获取所有一度好友,然后直接获取所有的二度好友,可能这样说有点抽象,如果说,先横向遍历所有一度,再横向遍历所有二度,是不是比纵向的遍历二度更快。
那么为了实现这样的广度优先遍历,那么我们就需要引入新的数据结构,队列。
也就是说,越早加入队列的节点越早的进行处理。形成一个先进先出的数据结构,
再有了这样的队列之后,我们就可以从队列的首位取出一个节点,然后讲其所有的子节点加入队列的末尾。
最后利用这个方式,我们可以不断的遍历,然后利用节点中的一个特定的标志位判断是否满足等于2度的节点,从而加入到结果集进行返回。