基础数学课7-动态规划
动态规划,其实类似于递归,递归是不断的分解问题,将复杂问题进行简化,而动态规划则是通过子问题的最优解,不断的推导,得到最终问题的最优解。而描述子问题向着最终解的状态转换表达式,则称为状态转移方程。
而寻找一个合适的状态转移方程,是动态规划的关键。
这里我们通过一个实际的案例,来解释如何通过动态规划来寻找最优解。
首先是判断两个单词之间的编辑距离
如果两个单词需要通过删除 增加 或 替换的方式,最终做到相等的,并且要求上述操作数要足够小,这种场景就很合适利用动态规划来进行处理。
对于这个场景中数据的数据的变化,我们总结了如下表格。

两个单词分别为mouse和mouuse
其中如果a串为1,b为0或者 a为0,b为1的时候,只需要进行一位的增加操作。
而除此外,如果都不为1,就需要考虑进行插入,还是删除或者替换,其操作可能为
2 1 0
而我们需要做的,就是不断的进行更新上面的图表,直到图表更新到了n – 1, m-1的地方。
那么我们书写一下上面的状态转换方程。
确定一个二维数组,d,其中结果位于d[i][j] i和j分别为最大的
如果x轴为0,y轴为0,那么 d[I,j]为0
如果x轴为0,y轴不为0,那么d[I,j]为i
如果x轴不为0,x轴为0,那么d[I,j]为i
如果两者都大于0,那么d[i][j] = min(d[i – 1, j] + 1 ,d[i,j-1] +1 , d[i- 1,j -1 ] + r(i,j))
其中的重点就在于d[i][j] = min(d[i – 1, j] + 1 ,d[i,j-1] +1 , d[i- 1,j -1 ] + r(i,j))
其中r(i,j)是判断当前的值是否相等,如果相等则为0,不相同则为1
于是最终形成如下的表格
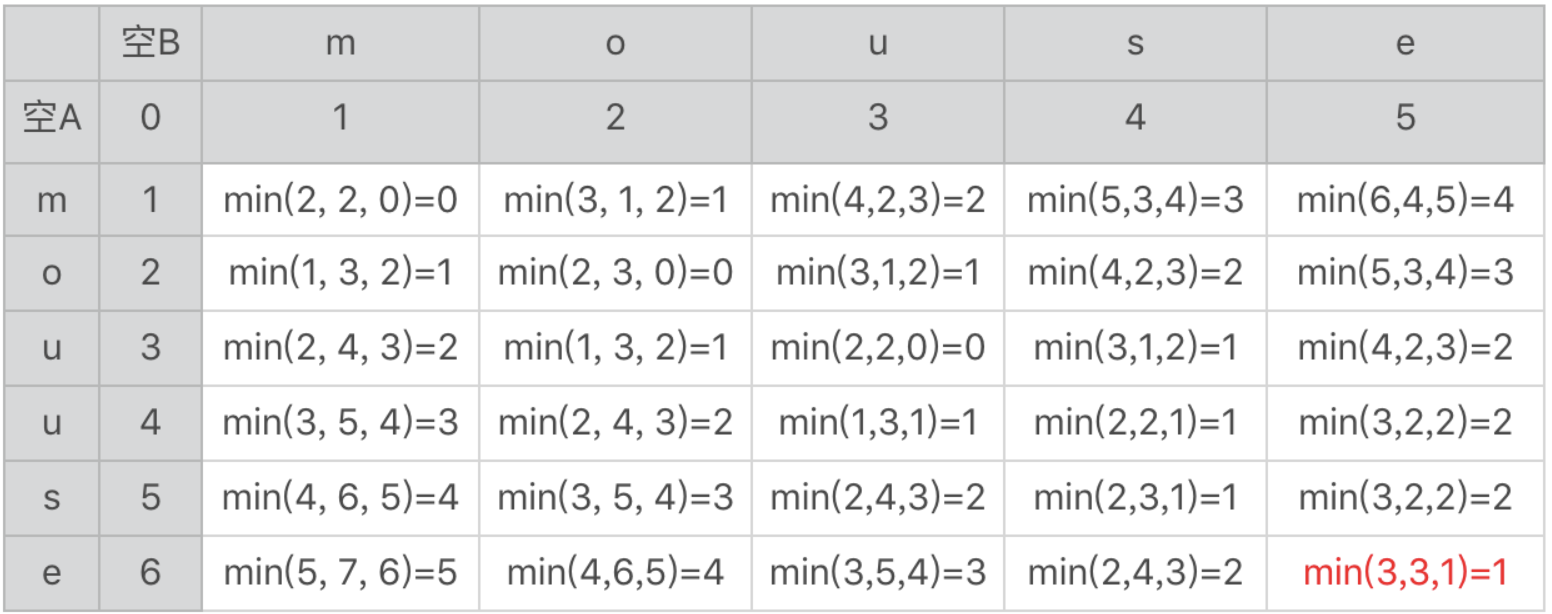
通过这个表格,我们可以看出我们通过动态规划来实现编辑距离的测算,可以保证查询的效率和效果。
除此外,还有着类似的问题,比如我们希望知道100块可以由至少多少个钱币组成
我们有 2,3,7 三种类型的钱币我们如何凑成100块
这时候我们就可以利用一个一纬数组来实现
这个一纬数组有101个下标,然后我们获取每一个下标的最小钱币数量,那么最后的结果就是最后一位下标的值
而我们每一位的计算,都可以通过当前位对应的值通过减去货币面值来获取到之前的最小值。
也就是 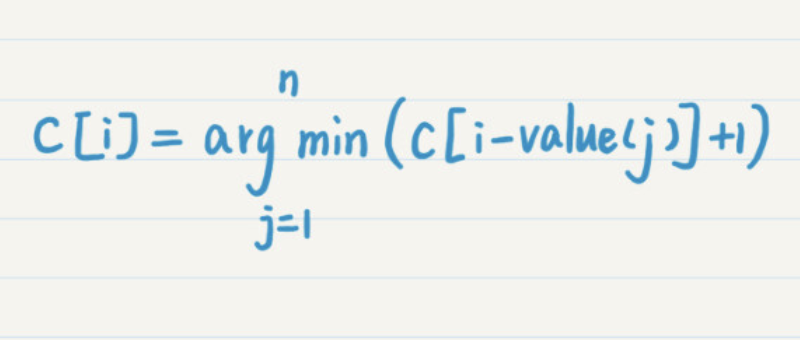
通过这个状态转换方程,来进行计算得到。
那么这个动态规划我们总结一下,就是不断的递归过程中,获取最优解,从而得到最优的答案。
只不过在此过程中没我们需要统计出一个转移方程。