7. 算法的特性
主要是有穷性,执行有穷的步骤后结束
然后是确定性,算法的每一步指定都必须要有确定的含义,不能含糊不清
其次是输入输出,输入可以为0到多个,输出必须要大于1
有效性,算法的每个步骤都有确定的功效,比如除法如果除以0,那么肯定是无效的
其次是时间的复杂度
时间复杂度大致可以理解为从开始到结束的时间
我们主要考试会分析的是算法对应的时间复杂度,常见的如下
![]()
空间复杂度则是一个算法在运行过程中需要占用的空间大小的度量,一个算法的空间复杂度只考虑运行过程中局部变量分配的空间大小
查找的两种方式
- 顺序查找法
- 二分查找法
我们首先说顺序查找法,也就是按照数组的顺序进行依次查找,如果找到了关键字为key的元素就返回成功,不然就认为失败
一般来说,查找的平均长度为
(N+1)/2
其次是二分查找法
要求数组是有序的,其查找的思路为,先确定区间的中点位置 min = (low + high) / 2
然后进行对比
如果大于了,则必然在mid的右子表,小于则在左子表,利用不断的递归进行查找,最终返回是否存在
一般的考试形式为
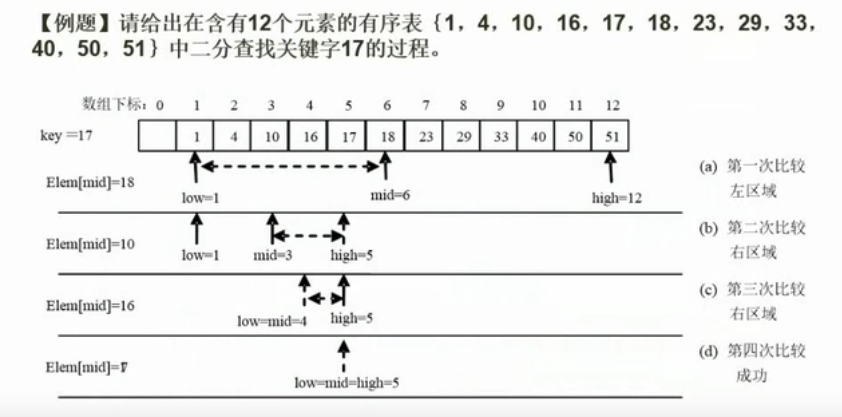
第一次先计算中位数,得到1+12 除以2 得到6.5 之后取整得到5
然后判断在左子表,中位重置为1+5 除以2 得到3
然后递归,得到4-5
之后是4
最后得到5,确定结果并返回
之后我们说下查找的另一种方式,这种方式和存储有关,名为散列表
散列表的基本思想为,有一个区间数组,下标为[0-n]
然后我们利用hash函数,将每一个输入,计算为区间下标中的一员
就比如0-9的区间
我们就可以利用
X % 5得到一个区间内的值,只不过需要考虑一点,也就是hash函数难免会有冲突
这时候我们可以使用一些解决方案
最简单的是开放定址法
就是依次查找这个地址后面是否存储了数据元素,如果不存在则存入数据元素
在完成了查找的基本概念介绍之后,我们看下排序这个概念
首先要介绍考试可能涉及的两个概念
稳定和不稳定性
稳定性指的是如果在一个数组中本来就有两个相同的元素,那么他们的相对位置,也就是谁前谁后在排序之前和排序之后是不会发生改变的
但是不稳定性就是可能发生改变
内排序和外排序
内排序排序本身不涉及到别的存储空间,自身就能办了
外排序则是排序需要借助别的空间进行排序
其次是排序的分类
- 插入类型排序,分为直接插入排序和希尔排序
- 选择类排序,分为直接选择排序和堆排序
- 交换类排序,分为冒泡排序和快速排序
- 归并排序
- 基数排序
接下来我们看下这些排序
直接插入排序
其基本概念就是每当遍历到一个元素,就和之前对比过的元素进行比较,然后确定插入的顺序,依次进行,简单明了
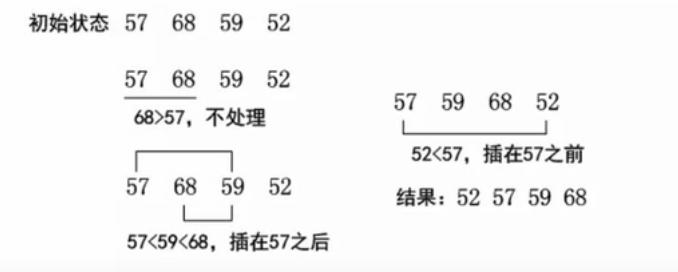
希尔排序

直接选择排序
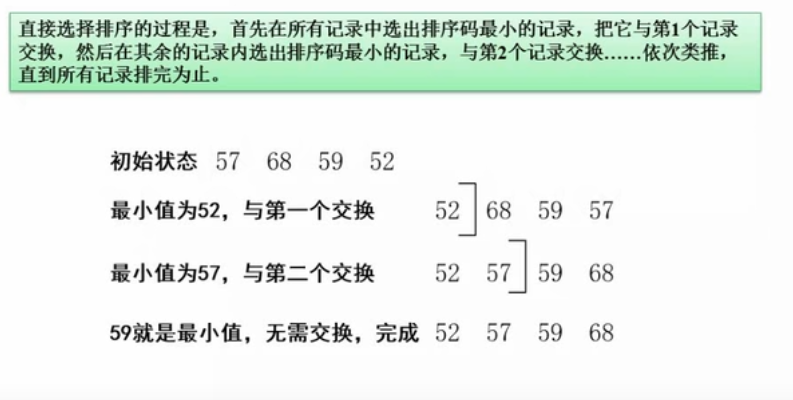
堆排序
利用二叉树维护的一种排序方式
对于堆排序,我们分为了大顶堆和小顶堆
概念如下
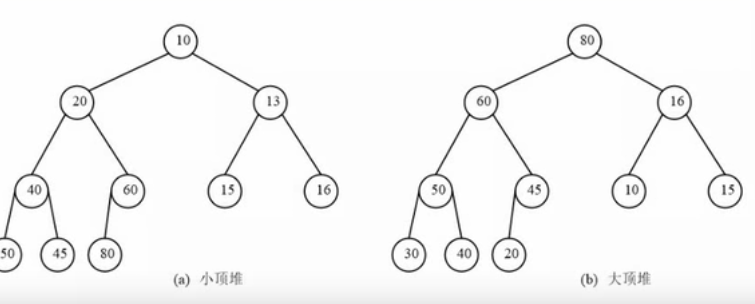
一种有序的完整二叉树的形式存在
那么其排序的方式就是
不断地从顶点取出最小的结点
然后不断地维护这个小顶堆
那么我们第一步先看如何维护这个堆
对于这样的一个树,我们要让其变为一个大顶堆吧
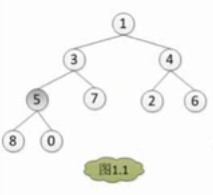
我们需要选择深度最深的非叶子节点,就是5,然后和其下最大的结点进行交换
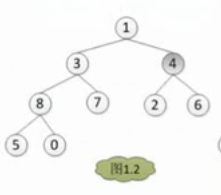
然后不断的进行选取,当我们选择到了3的时候,我们需要将3和8 交换,然后依次向下递归
组成这样
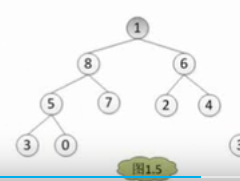
最后直到根节点,然后依次向下递归,确定一个大顶堆
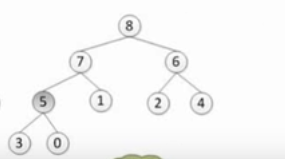
那么其排序就很简单了
只要不断地取根节点,并将叶子节点进行交换
然后重新组成堆即可
不过这方式并不强,因为维护一个堆本身就近似有序了
其次是冒泡排序

和快速排序

归并排序
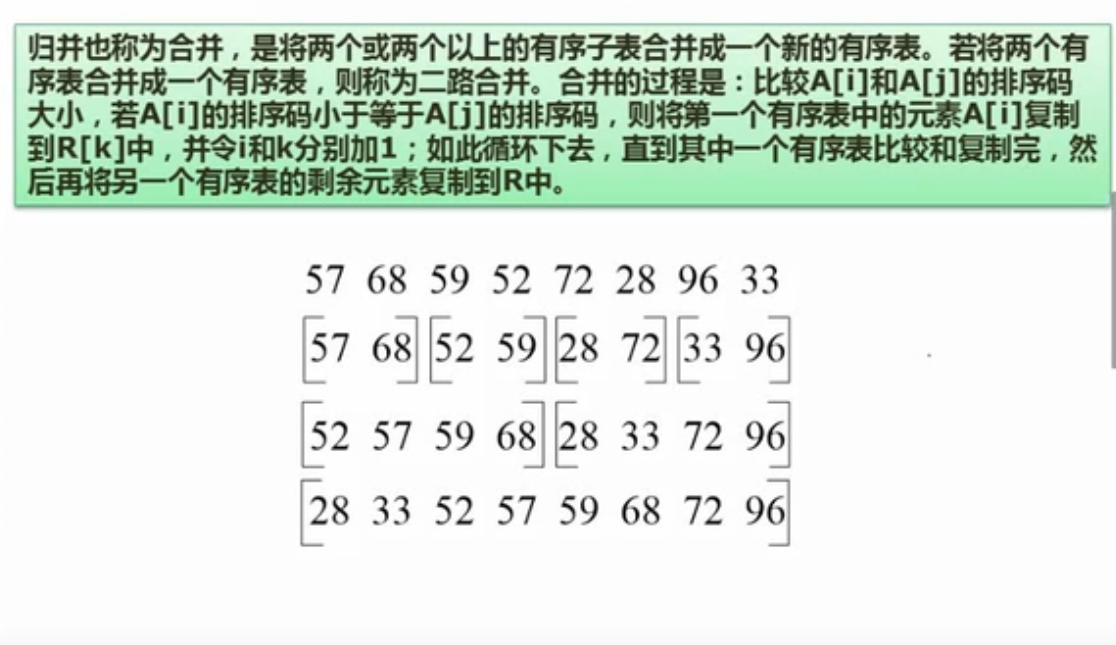
还有主要会将的基数排序
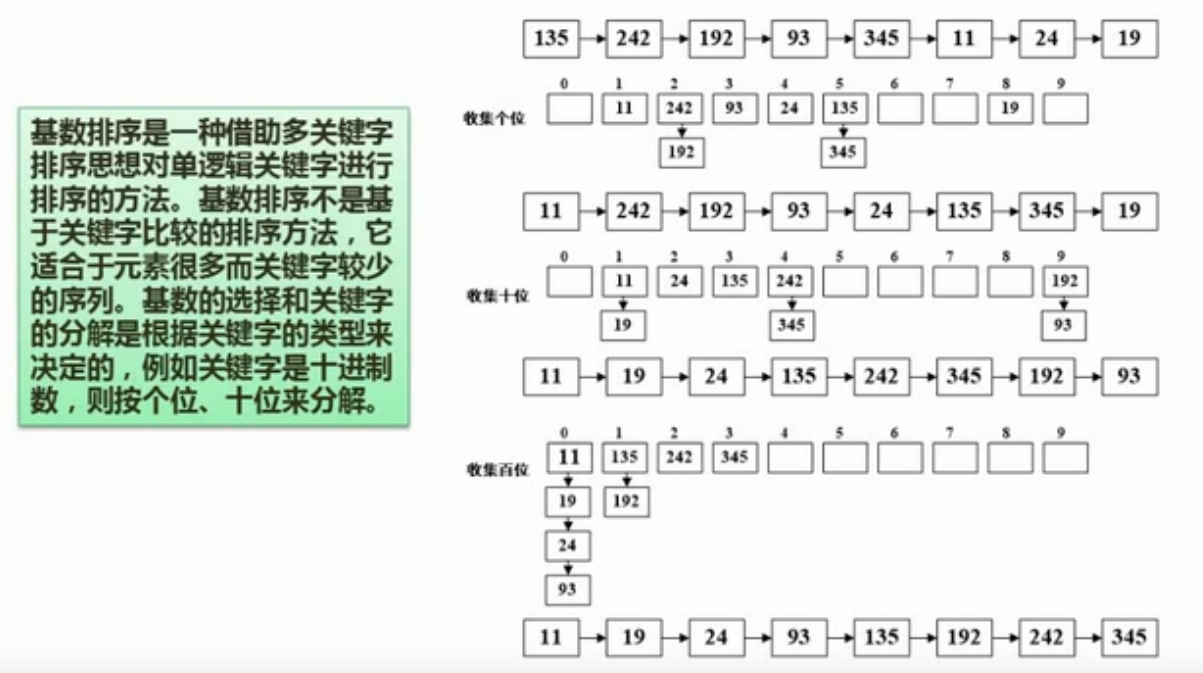
这种方式是利用了将原本一个多位的数字拆分为单位数字的方式来做的
我们先对个位排序,形成散列表
然后展开后对十位进行排序,形成散列表
然后对百位进行排序,形成散列表之后展开
这种方式进行排序,最终完成有序队列
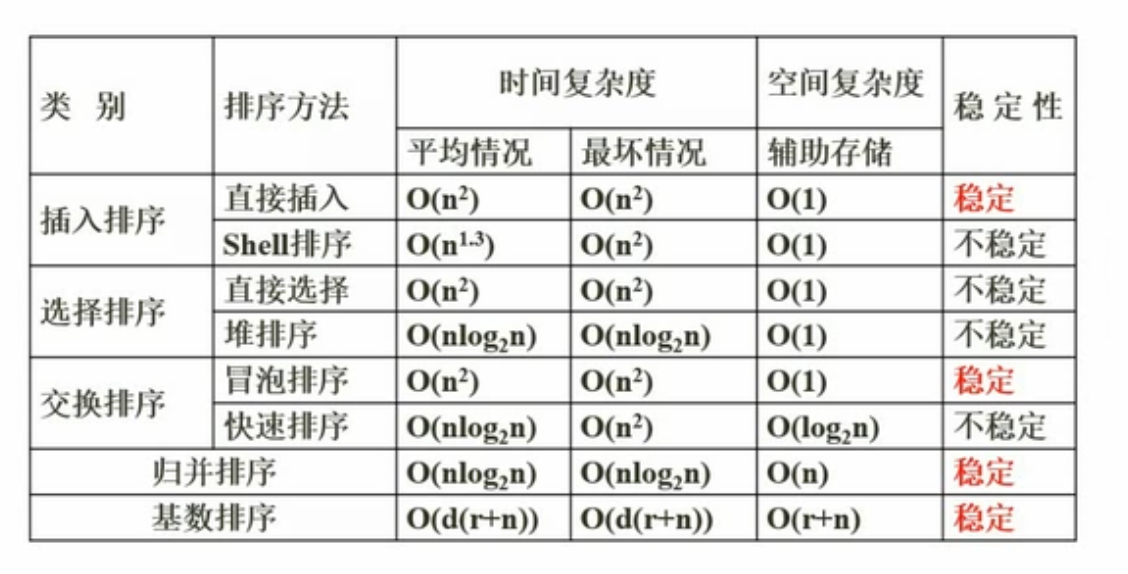
最后给出一个各个算法的复杂度对比图
这也是选择时候经常考的一道题