数据结构和算法
- 概述
对于这一章,我们首先了解一些概念
先是数组和矩阵,我们会了解基本概念,并且了解其在内存的计算方式
然后是线性表,其常见的队列和栈的概念,以及其相关的计算题
广义表,只是了解其基本定义即可
树和二叉树,了解基本概念和使用场景
图,一种特别的数据结构,只需要了解其定义
排序和查找算法,需要详细了解相关的算法和计算题
- 数组
对于数组,我们主要了解其计算方式,一般来说,分为一维数组和多维数组
对于一维数组的计算方式,可以简化为 a+i*len
对于多维数组,比如a[m][n],如果是按行存储,计算方式为 a + (i* n+j) * len
如果是按列存储,则计算方式为a + (j*m + i) * len
比如5行5列的二维数组,按行存储,每个元素占两个字节,那么a[2][3]的存储地址为
(2*5 + 3 ) * 2
- 矩阵
对于矩阵,经常考试的是稀疏矩阵,其可以分为上三角矩阵和下三角矩阵
计算公式也不一样,上三角的为(2n – i + 1)* i/2 + j
下三角的为(i + 1)* i/2 + j
这样背公式进行计算也可以,或者使用带入法,这里以例题举例

上面的图进行计算的话,首先带入A0,0
一般得到的是应该是 M1才是,因为数组从M1-Mm
带i=0 j=0,可以排除B C
然后再代入A1,1,应该得到M3,故得到D是正确的答案
- 基本的数据结构定义
可以分为线性结构
比如数组和列表
非线性结构,比如树或者图
- 线性表的定义
常见的数据结构有 顺序表和链表
对于顺序表,基本的表现形式如下
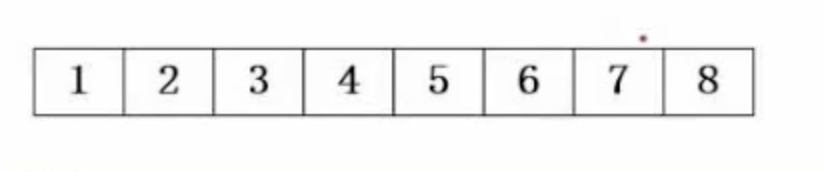
其次是链表,分为了单链表和循环链表和双向链表
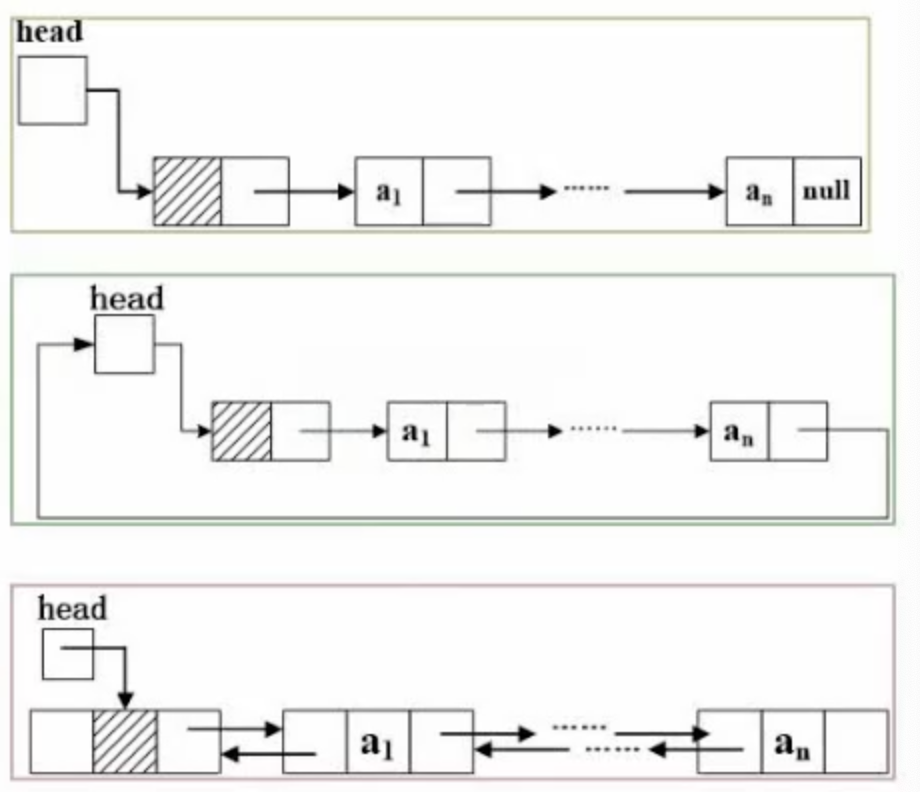
单链表是依次查找
对于循环链表,则是在链表的结尾处有一个指向head的引用
对于双向链表,则是每个节点都保留前一个和后一个的引用
对于不同的链表,主要的考试形式是考验不同类型的链表的插入和删除形式

然后是链式存储和顺序存储的对比,基本可以如下
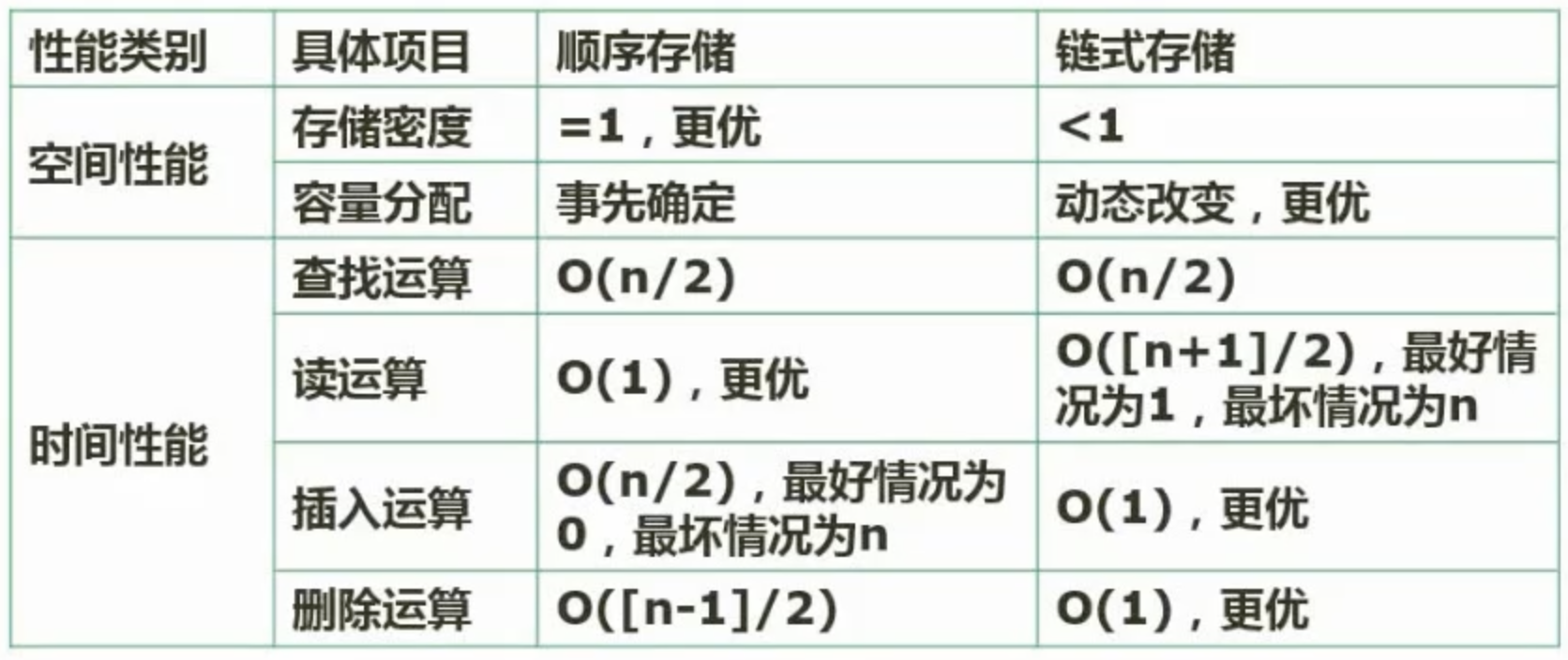
比如存储密度来说,数组更加占有,因为链表需要存储引用
而数组,需要提前分配内存,从这方面链表更加的灵活
对于时间性能,则是查找的一样的性能,都需要遍历
对于读取,如果知道下标,则数组更快,除此外。
但是对于插入,因为数组可能涉及到往后插入,所以性能并不强力
同理删除也是
对于队列和栈来说
存取的方式不一样,一个是先进先出,一个是先进后出
对于队列就是先进先出,对于栈来说,就是先进后出
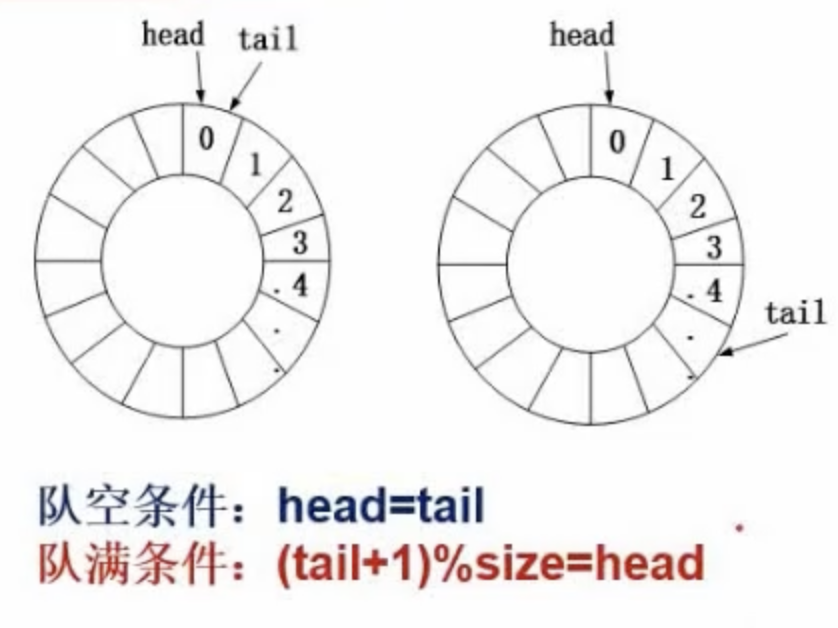
然后是一个特别的数据结构,循环队列
这个队列判断队空和队满的方式很好玩,基本如上的计算,如果head=tail就是队空
如果是tail + 1 % size = head就是队满
这里我们看一个例题,一般是求出队顺序的题
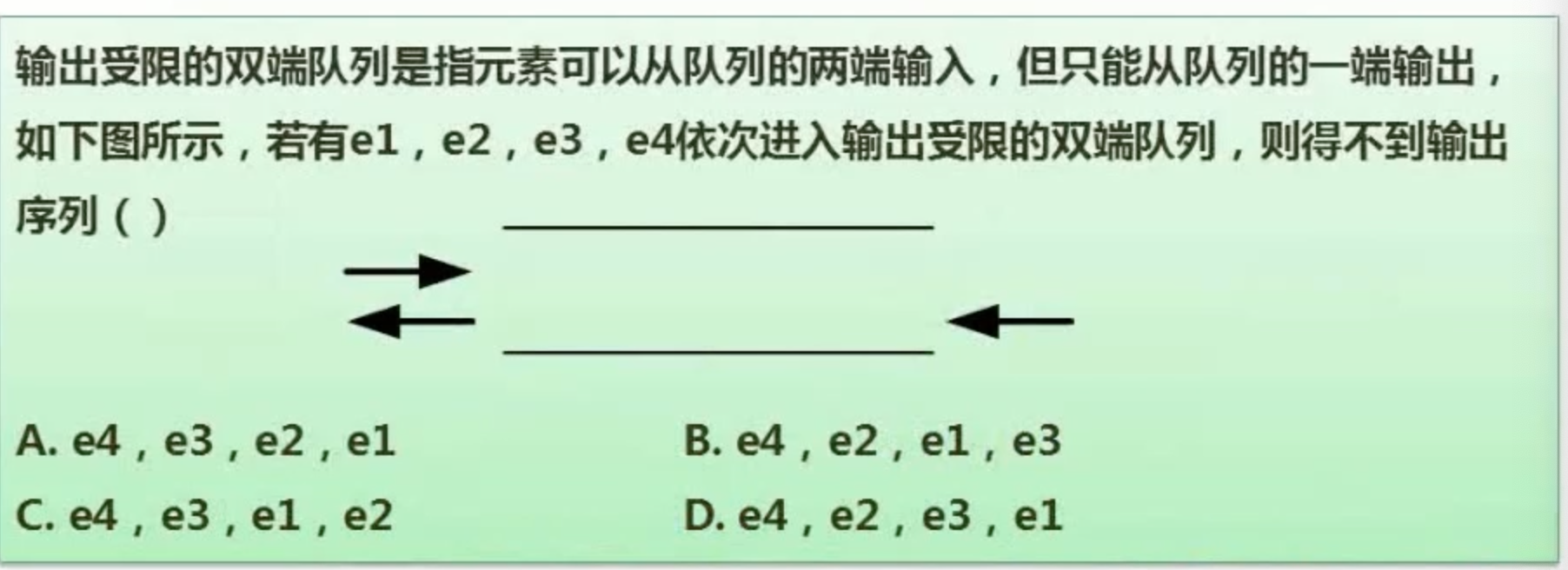
上面这道题,我们可以直接排除e4
然后看剩下三个顺序
对于e3 e2 e1,只需要全部从左侧进队即可
对于e2 e1 e3,只需1和2从左侧,3从右侧进队即可
对于e3 e1 e2,只需要1 2从右侧进队,3从左侧进队即可
然后是广义表这个概念
一般是n个表元素组成的有限序列,是一种以递归形式定义的,

其中a是数据元素,可以是一个单一元素,也可以是一个子表
然后是一些概念
长度:是最外层包含的元素个数
深度:递归定义的重数
然后是head和tail的概念,head是表头,tail是除了表头之外的全部数据
就比如有一个广义表 LS1=(a,(b,c),(d,e))
Head就是 a, tail就是 (b,c),(d,e)
长度就是3,深度就是2
如果希望取出b字母,则需要进行 head(head(tail()))
查找二叉树
是二叉排序树的一种,这个树中,遵循左孩子小于根,右孩子大于根的定义
在这个树中,如果是插入,则首先根据二叉树进行查找,如果已经存在,则不再插入
这个查找的过程会不断地进行比较,然后选择左子节点或者右子节点,直到叶子节点
如果是删除,则需要判断,如果删除的节点是叶子结点,直接删除
不然就是查找左子树查找关键值最大的结点s,然后让其和删除节点替换后删除应该删除的节点
哈夫曼二叉树,用于无损压缩的二叉树
主要是了解一些概念,了解如何做题
对于概念,则是需要了解树的路径长度,权,带全路径长度

从15-2中需要走两个节点的距离,所以路径长度就是2
每个节点上的数字就是权
计算带权路径长度,假设2,节点,权重是2,长度是2,带权路径长度就是4
树的代价就是所有带权路径长度之和
需要注意的是霍夫曼二叉树,只有叶子节点是真的,中间节点是用方便计算的虚拟节点
然后考题除了计算总代价
还有构造哈夫曼树,只需要记住一点,约小的节点越靠下,比如

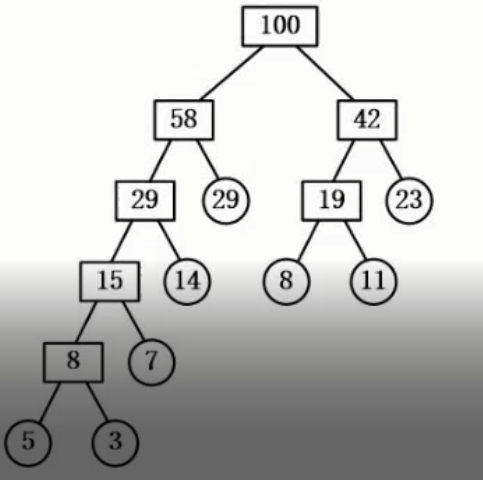
线索二叉树
二叉链表的存储结构,只能找到该结点的左右孩子,不能得到该结点在遍历过程中的遍历前驱和直接后继结点。二叉链表存储二叉树时,有2n个指针域,其中n+1个都为空指针域。
利用空指针域存储结点遍历过程中的前驱和后继结点,使结点之间组成联系,在遍历的过程中可以不用通过栈或递归。
线索 二叉树的作用:
将树转换成线性链表,二叉树在首次遍历中线索化,在需要时可以直接获得结点的前驱和后继,不需要像栈一样频繁的压栈出栈。
可以分为
前序线索二叉树,中序线索二叉树,后序线索二叉树
按照前序和中序,后序进行划分,

最后是平衡二叉树
主要是为避免二叉树的倾斜,提出了平衡二叉树的定义
任意结点的左右子树的深度之差不超过1,