我们说了基本的特征处理函数,而且拿线性回归模型进行了对比,但在实际的应用中,线性关系比较少,就好比房屋属性和房屋价格并不是单纯的线性关系,这就是为嘛在房价预测的任务上,误差居高不下。这种情况下,就需要考虑其他类型的模型算法,尤其是非线性模型
我们就大致讲下Spark MLlib框架中支持的不同模型
首先按照样本是否可以预测Label,机器学习可以分为监督学习和非监督学习
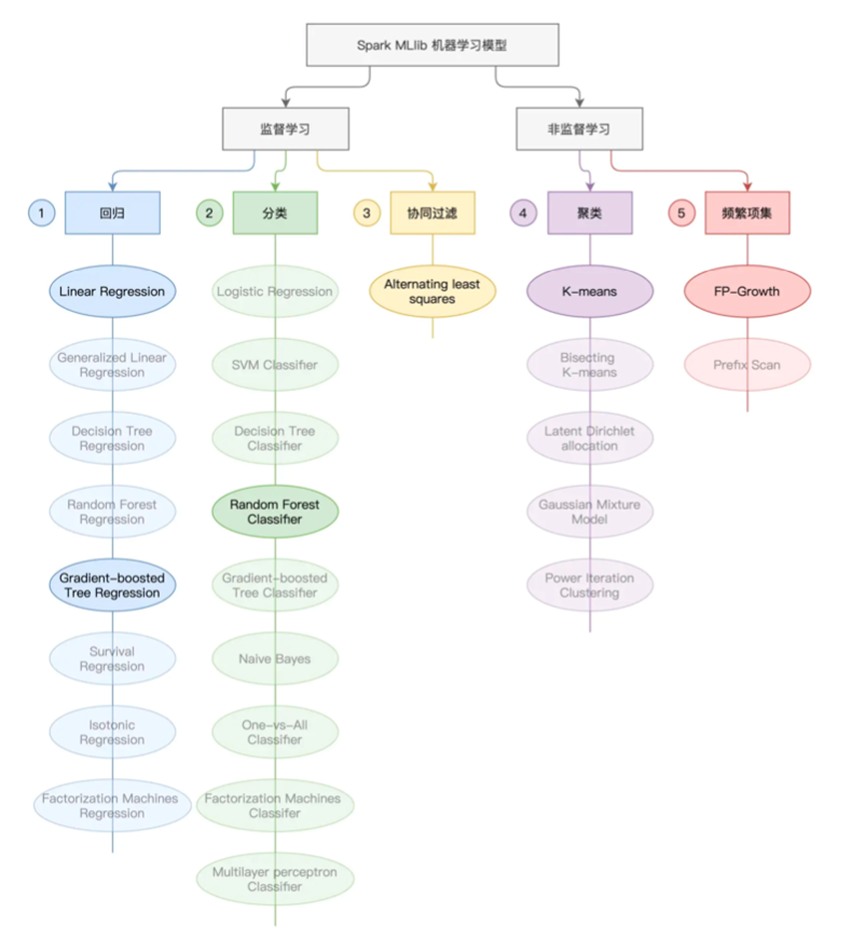
总共可以分为了回归,分类,协同过滤,聚类,频繁项集
为了介绍这些不同种类的模型,我们需要先搞清楚决策树,GBDT RF这些前置知识点
我们首先介绍决策树的概念
决策树的概念可以理解为是一种根据样本特征而构建的树形结构,决策树内部包含节点和有向边,节点中存在着内部节点和叶子节点
内部节点代表着样本特征,叶子节点代表着分类,比如我们拿上一节的房屋预测中的居室数量和房屋面积两个特征来进行分类
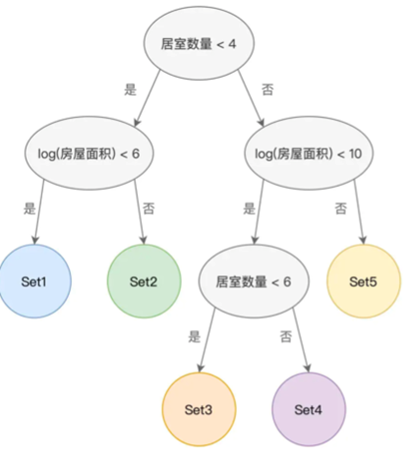
其中的每个节点都是一个特征,然后拥有两个边,代表符合和不符合
最终到达叶子节点,叶子节点存着数据样本的分类,其中包含着若干的数据样本
这样我们有了5个子集,就可以去解决分类或者回归问题了,简单点,我们可以分为差,一般,好,很好,极好
这样我们有一个新的房屋的时候,可以直接确定其是属于哪一类的
或者说当预测房价的时候,只需要根据决策树,确定是哪个节点的,最终去取这个节点的平均房价均值
在说完这个之后,我们就可以思考一个问题,这样的决策树是如何创建出来的?
这就需要引入一个纯度的概念,如果子集中的所有标签都一样,那么这个标签的多样性就是1,这个集合的样本纯度就很高,当构建决策树的时候,会遍历所有的特征,进行提纯,这样的提纯的目的就是如果分割后的子集纯度越高,其提纯能力就越高
基于这种逻辑,我们可以依次筛选提纯能力最高,次高,第三高的特征,逐步去构建决策树,而且为了避免树深度过深,我们可以人为的设置纯度阈值,或者指定深度限制
那么我们接下来引入两个算法,来提高纯度,创建决策树
首先是Random Forest
随机森林,其设计思路是三个臭皮匠,赛过诸葛亮
主动的训练多个决策树,彼此之间相互独立,不存在任何的依赖关系,对于每一颗树,都会选择部分样本和特征进行训练,这就是随机的由来
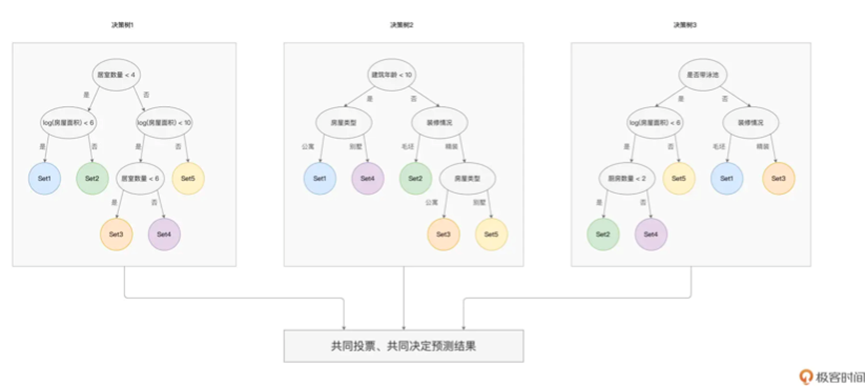
当需要进行新的样本预测时候,就同时将样本喂给多颗树,然后获取到预测结果
就比如三棵树,分别落在了Set3,Set2,Set3 那么最终结果就是Set3,并根据这个子集获取均值
其次是GBDT,和随机森林类似,都是根据多棵决策树来拟合数据样本,树和树之间是有依赖关系的
每一颗树的构建都是基于前一颗树的训练结果,也就是站在前人的肩膀上看的更远
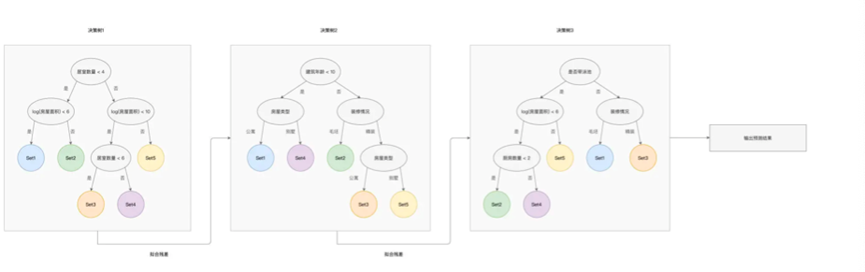
每一颗新树的构建都基于上一颗树的样本残差

只要不断的进行新树的构建,就可以最终趋于真实值,不过在这种情况下,需要担心过拟合问题,也就是在训练集上过分拟合,导致不如人意,要做到这样一点,我们就需要限制决策树的数量和深度,来降低GBDT的复杂度
在讲述完成这两者之后,我们就可以看一些经典的算法用法
比如对于房屋这一个数据,我们首先进行一个房价的预测,这里我们直接采用GBDT进行拟合,基本代码如下
// numericFields代表数值字段,indexFields为采用StringIndexer处理后的非数值字段 val assembler = new VectorAssembler() .setInputCols(numericFields ++ indexFields) .setOutputCol(“features”) // 创建特征向量“features” engineeringDF = assembler.transform(engineeringDF) import org.apache.spark.ml.feature.VectorIndexer // 区分离散特征与连续特征 val vectorIndexer = new VectorIndexer() .setInputCol(“features”) .setOutputCol(“indexedFeatures”) // 设定区分阈值 .setMaxCategories(30) 17 // 完成数据转换 engineeringDF = vectorIndexer.fit(engineeringDF).transform(engineeringDF) |
我们利用了一个VectorIndexer在创建特征字段之后进行了进一步的转换
其负责帮助决策树相关算法,进行区分离散特征和连续特征,为什么要区分呢?就好比我们直接将街道类型转换为数字之后,会引入原本不存在的大小关系
为了解决这种不应该存在的大小关系,就需要将其标记为为离散特征,说明不存在任何关系
这里我们使用了VectorIndexer进行处理,使用了setMaxCategories方法,设置了阈值,我们设置了30,也就是多样性大于30的特征,就是连续特征,否则则是离散特征。
这样,我们就区分了离散特征和连续特征,进行了提纯
之后我们就可以利用GBDT进行拟合了
import org.apache.spark.ml.regression.GBTRegressor 2 // 定义GBDT模型 val gbt = new GBTRegressor() .setLabelCol(“SalePriceInt”) .setFeaturesCol(“indexedFeatures”) // 限定每棵树的最大深度 .setMaxDepth(5) // 限定决策树的最大棵树 .setMaxIter(30) 11 // 区分训练集、验证集 val Array(trainingData, testData) = engineeringDF.randomSplit(Array(0.7, 0.3)) // 拟合训练数据 val gbtModel = gbt.fit(trainingData) |
我们设置了setMaxDepth和setMaxlter,前者限制了每棵树的深度,后面限制了决策树的总体树木,然后利用fit函数进行训练
其次是房屋分类
我们这里还是使用房屋数据进行测试,我们进行房屋分类
这里我们使用房屋质量作为Label 标的特征

我们接下来就利用随机森林模式,拟合训练数据
代码进行如下
import org.apache.spark.ml.regression.RandomForestClassifier 2 // 定义随机森林模型 val rf= new RandomForestClassifier () // Label不再是房价,而是房屋质量 .setLabelCol(“indexedOverallQual”) .setFeaturesCol(“indexedFeatures”) // 限定每棵树的最大深度 .setMaxDepth(5) // 限定决策树的最大棵树 .setMaxIter(30) // 区分训练集、验证集 val Array(trainingData, testData) = engineeringDF.randomSplit(Array(0.7, 0.3)) // 拟合训练数据 val rfModel = rf.fit(trainingData) |
然后我们进行训练,取准确度,测试拟合结果
import org.apache.spark.ml.evaluation.MulticlassClassificationEvaluator 2 // 在训练集上做推理 val trainPredictions = rfModel.transform(trainingData) // 定义分类问题的评估对象 val evaluator = new MulticlassClassificationEvaluator() .setLabelCol(“indexedOverallQual”) .setPredictionCol(“prediction”) .setMetricName(“accuracy”)
// 在训练集的推理结果上,计算Accuracy度量值 val accuracy = evaluator.evaluate(trainPredictions) |
之后我们再说下非监督学习
非监督学习,专门代指为数据样本中没有Label的机器学习
如果没有Label,这样的学习有什么意义呢?其实还是有用的,比如使用K-meas算法进行分类,对电影进行更细致的聚类
这里我们进行聚类
我们去掉了SalePrice和OverallQual两个字段,进行了聚类
import org.apache.spark.ml.clustering.KMeans val kmeans = new KMeans().setK(20) val Array(trainingSet, testSet) = engineeringDF .select(“features”) .randomSplit(Array(0.7, 0.3)) val model = kmeans.fit(trainingSet) |
K-meas的使用很简单,指定K值即可
我们设置了20个不同的类别,进行训练
这样我们获得了K-means的训练结果,我们可以拿这个新字段,参与到后续的监督学习中,进行优化提升
最后我们引入Spark MLlib支持的协同过滤和频繁项集算法,这里我们使用电影推荐数据进行测试,通过不同的算法构建简易的电影推荐引擎›
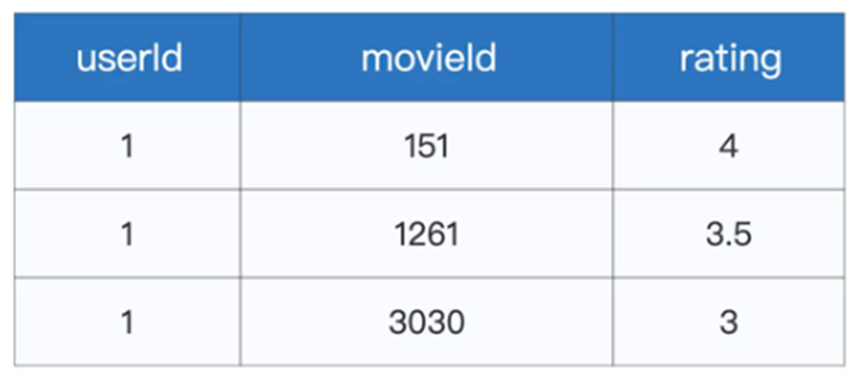
这份数据分别代表着不同用户对着不同电影的打分,但是我们可以按照两个维度进行拆分,分别是用户和电影,由于存在着不同的维度,所以我们可以构建出不同的推荐引擎
首先我们尝试构建协同过滤,其核心含义是相似的人倾向于喜好相似的物品集
只需要挖掘出用户和用户之间的相似性,以及物品和物品,用户和物品直接的相似性,就可以进行推荐了
那么这些相似性的量化方式就是矩阵分解
按照用户和物品两个矩阵可以拆分为不同的Embedding,之后我们就可以使用欧氏距离或者余弦夹角的方式进行计算相似度
那么我们直接上代码来看
首先准备数据集
import org.apache.spark.sql.DataFrame 2 // rootPath表示数据集根目录 val rootPath: String = _ val filePath: String = s”${rootPath}/ratings.csv”
var data: DataFrame = spark.read.format(“csv”).option(“header”, true).load(filePa 8 // 类型转换 import org.apache.spark.sql.types.IntegerType import org.apache.spark.sql.types.FloatType // 把ID类字段转换为整型,把Rating转换为Float类型 data = data.withColumn(s”userIdInt”,col(“userId”).cast(IntegerType)).drop(“userId data = data.withColumn(s”movieIdInt”,col(“movieId”).cast(IntegerType)).drop(“movi data = data.withColumn(s”ratingFloat”,col(“rating”).cast(IntegerType)).drop(“rati // 切割训练与验证数据集 val Array(trainingData, testData) = data.randomSplit(Array(0.8, 0.2)) |
然后准备拟合模型
import org.apache.spark.ml.recommendation.ALS 2 // 基于ALS(Alternative Least Squares,交替最小二乘)构建模型,完成矩阵分解 val als = new ALS() .setUserCol(“userIdInt”) .setItemCol(“movieIdInt”) .setRatingCol(“ratingFloat”) .setMaxIter(20) val alsModel = als.fit(trainingData) |
我们设置了两个维度之后,就可以获取到ALS模型的训练结果了
import org.apache.spark.ml.evaluation.RegressionEvaluator 2 val evaluator = new RegressionEvaluator() // 设定度量指标为RMSE .setMetricName(“rmse”) .setLabelCol(“ratingFloat”) .setPredictionCol(“prediction”) val predictions = alsModel.transform(trainingData) |
之后是频繁项集
也是一类非监督学习的范畴,用于挖掘数据集中经常成群结对出现的数据项,并建立关联规则,从而为决策提供数据
也就好比,如果某几种物品经常是配对购买的,那么这就是一个数据项
回到电影,那么我们也可以对电影进行关联,比如金刚川 八佰 经常一起出现在某人观影列表,这就是关联关系
那么我们如何进行这样关联关系的构建呢?
首先我们需要以用户为粒度,进行收集电影集合

其实本质上就是一行代码
val movies: DataFrame = data.groupBy(“userId”).agg(collect_list(“movieId”).alias(“movieSeq”))
.select(“movieSeq”)
这样就构建好了数据集
然后我们就可以借助Spark MLlib来完成频繁项集的计算
val fpGrowth = new FPGrowth() // 指定输入列 .setItemsCol(“movieSeq”) // 超参数,频繁项最小支持系数 .setMinSupport(0.1) // 超参数,关联规则最小信心系数 .setMinConfidence(0.1) val model = fpGrowth.fit(movies) |
这样我们进行拟合了频繁项集模型,其中设置了两个参数,分别是setMinSupport的最小支持系数和最小信心系数
这个最小支持系数,可以如下理解,假设我们有7000名用户,其中 八佰加金刚川的组合出现次数超过了700次,才被认为是频繁项
相应的最小信心系数也是类似,也是用于挖掘关联规则的,同理如果系数越高,挖掘的关联关系越少
最后我们就可以获取到相关的频繁项和关联关系
model.freqItemsets.show(1)

model.associationRules.show(1)
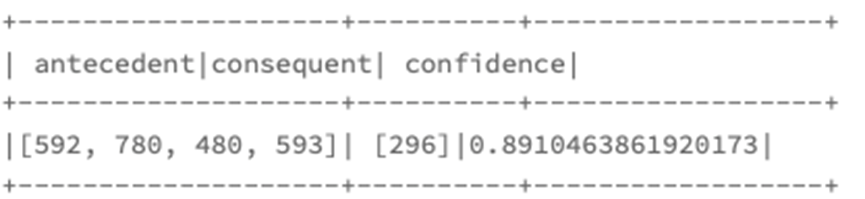
这样我们就实现了基本的频繁项集模型
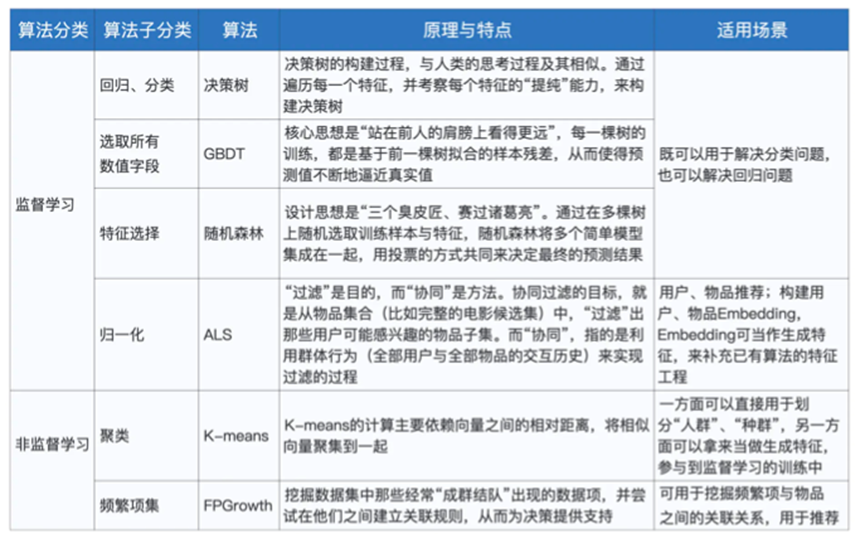
到此我们基本讲完了MLlib相关知识,我们将算法的分类和原理,特点整理如下