加权图就是图上每个边都关联一个权值或者成本的图模型
例如在航线中,一个边可能就是距离或者维护费用
所以,经常利用加权图来计算如何让成本最小化
引入了生成树这个概念
最小生成树:
即为一个权值(所有边的权值之和)最小的生成树
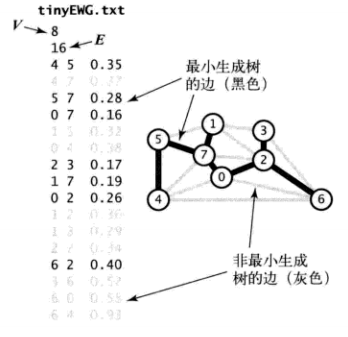
在这一章关于加权图的学习中
1.对应最小生成树,只考虑连通图,最小生成树只可能存在连通图中,如果不是连通图,则只能计算所有连通分量的最小生成树
2.权重和距离不一定成正比,两者没有直接关系
3.边的权重可能为0或者负值
4.所有边的权重不相同
不先进行相同权重的假设
那么我们如何获取到最小生成树呢,在此处引入切分的定理
切分定理会把加权图的所有顶点分成两个非空且不重复的集合.
横切边则是则是一条连接着两个不同集合的顶点的边
那么我们得到一个结论
给定任意的切分,它的横切边的最小权重必然在图的最小生成树中
利用上述观点,引入了贪心算法
使用切分定理找到最小生成树的一条边,然后不断重复直到最小生成树的所有边
使用图片表示的话
就是将所有边初设设置为灰色,然后进行切分,产生的横切边中寻找权重最小的,然后标为黑色
如此反复,直到标记了V-1条黑色边
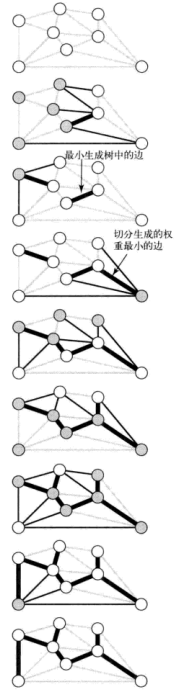
那么学习贪心算法之前,先看如何实现加权无向图
先列出一份API
首先是边相关的API,边是构成图的一部分

然后是图的API

从上面的API可以看出来
首先我们实现了comparato方法,具有了比较的方式,让一个图可以按照权重排序
有一定的缺点,会给对象带来一定的开销,而且整体结构中一定会保存两次相同的edge对象
然后是最小生成树的实现

实现的第一种算法名为Prim算法,简单说就是算法的每步都是为一个正在生长中的树添加一条边,一开始树中只有一个顶点
然后向他添加V-1条边,每次都是在下一条连接树中的顶点且另一边不在树中的的边中挑选权重最小的边添加进去
我们对此还设置了对应的要求
对于顶点,使用了一个布尔类型的数组marked[],如果顶点V在树中,marked[V]为true
对于边,有两种考虑,一种是以一条队列mst来保存最小的生成树的边,
或者一个由顶点索引的edge对象数组 edgeTo[]来保存,其中 edgeTo[V]表示将V连接到树中的edge
对于横切边,使用一个优先队列 MinPQ<Edge>来比较所有的边
排序如下
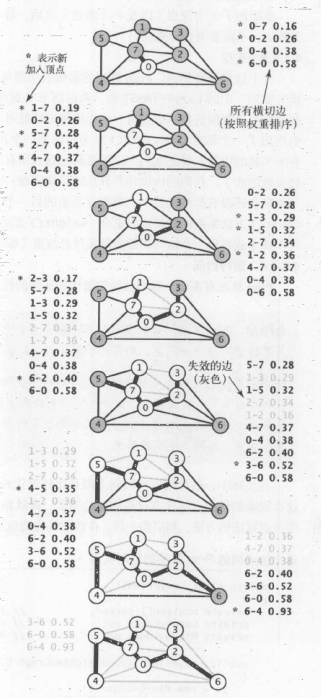

整体流程就是每次都将队列中最小的权重的边加入进树,将新加入的顶点的边加入优先队列
然后每次遍历队列里,移除多余的边
直到添加了V-1个边及V的顶点之后,最小树完成了,故直接抛弃优先队列
具体的实现如下
public LazyPrimMST(EdgeWeightedGraph G) {
marked = new boolean[G.V()];
pq = new MinPQ<Edge>();
mst = new Queue<Edge>();
Visit(G, 0);//添加第一条
while (!pq.isEmpty()) {//只要不为空
Edge edge = pq.delMin();//删除最小值
int v = edge.either(), w = edge.other(v);
if (marked[v] && marked[w])
continue;
mst.enqueue(edge);//添加到边
if (!marked[v]) {//将边添加到树中
Visit(G, v);
}
if (!marked[w]) {
Visit(G, w);
}
}
}
private void Visit(EdgeWeightedGraph G, int V) {
marked[V] = true;
for (Edge n : G.adj(V)) {
if (!marked[n.other(V)]) {//如果另一条边每标记过
pq.insert(n);
}
}
}
没有实现的是每次Visit过程中,关于从队列中移除
这是因为我们真正感兴趣的只是树节点和非树节点中权重最小的边
所以我们只需要在优先队列中保存所有从W到树顶点中权重最小的边(反正其他的边迟早会失效)
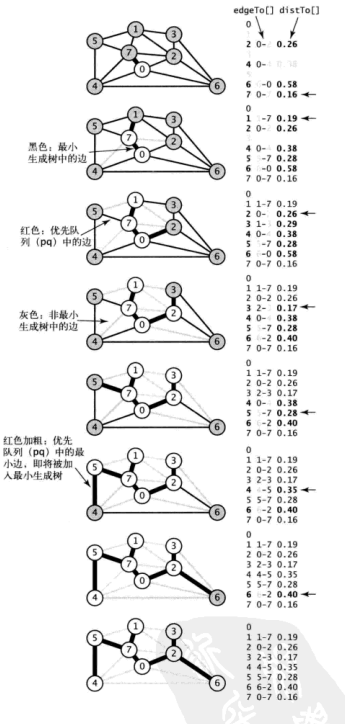
实现优化,需要我们将marked[]和mst[]这两个数组替换为edgeTo[]和distTo[]
edgeTo[]是为了保存一个不在树中顶点和树相连的权重最小边
distTo[]是为了保存对应边的权重
优先队列关联edgeTo[v]边的权重
实现的具体为:
先取出一个边v,然后搜索它的邻接链表中的每一条边v-w,如果w不在队列中且v-w权重小于已知的edgeTo[w]
进行更新,然后将v-w连接上树


还有就是
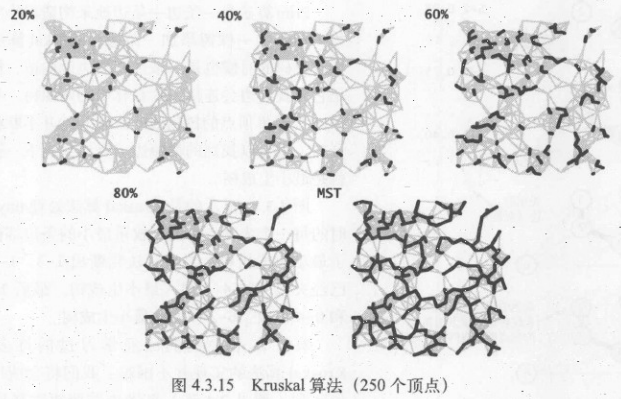
Kruskal算法
这一个算法的基本思想为按照边的权重顺序(从小到大)处理
逐步把最小的边加入树中,保证加入的边和已有的边不会构成环,直到含有V-1个边
即创建一个优先队列保存所有的权重,一个union-find数据类型来识别已经保存的边,一个队列保存所有最小生成树的所有边
然后从小到大的顺序遍历权重,添加到最小生成树的队列,同时用union-find数据类型识别是否可以被添加进去
这里就是用到了触点方案进行处理
简单实现如下
public KruskalMST(EdgeWeightedGraph G) {
mst = new Queue<Edge>();
MinPQ<Edge> pq = new MinPQ<Edge>(G.edges());
UF uf = new UF(G.V());
while ((mst.size() < G.V() – 1) && (!pq.isEmpty())) {// 如果不为空且数量小于V-1
Edge edge = pq.delMin();
int v = edge.either();
int w = edge.other(v);
if (uf.connected(v, w))// 如果已经存在,pass
continue;
uf.union(v, w);// 并上权数
mst.enqueue(edge);// 添加上去
}
}
各种无向加权图的性能对比如下
