简单描述一下加权有向图
在现实生活中,我们经常要从一个地点到另一个地点,手机app总是能很好的计算出最短路径
这时候就要考虑加权有向图的路径问题了
在之前,我们思考过一个顶点是否可以到达另一个顶点,在这里面我们考虑了权重问题,
每条路径都有一条与之相关的路径权重
本章的重点
1.加权有向图的API及查找路径的API
2.经典Dijkstra算法
3.在无环加权有向图中快速解决,可以允许边的值为负的AcyclicSP
4.Bellman-Ford算法:允许图有环,权值可以为负的
我们先不考虑平行边或者自环问题
最短路径不一定唯一,所以我们只考虑一个
权重不一定等于距离,我们只是再找权重或者成本最短的路径
最短路径一般都是简单的
而且不考虑负权重问题

这就是最短路径树
尽管这个树中可能有相同长度的路径,如此情况,只需要删除其中一条路径的最后一条边
通过构造这颗最短路径树,可以获取从s到可以到达的任何顶点的最短路径
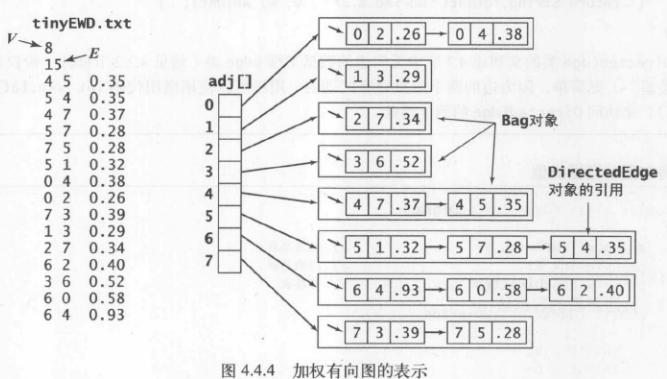
有向加权图的边的API

有向加权图的api

对于寻找最短路径的问题
我们设计了如下的api

创建一个最短路径树,并计算最短的长度
对于此api,仍然选择了使用一个由顶点索引的DirectedEdge对象的父链接数组 edgeTo[],其中保存着索引v和父节点的边
再加上一个记录路径长度,由顶点索引的数组distTo[],其中v则是表示由起点s到顶点v的已知最短路径
同样再加上约定的条件,设定起点的值为null,距离为0
再引入一个概念:
我们先将distTo中的所有元素除了0,其他的都设置为无限大,这样方便比较,
再说一个松弛,放松边v-w意味着 我们看s到w的最短路径是否先从s到v,然后v到w.
即v-w的路径为distTo[v]和e.weight的和.如果小于distTo[w],则更新distTo[w]

有了这个放松的实现,我们来看下对应的最小路径树是如何实现的
1.Diijkstra算法:
Diijkstra算法采用了类似的方法计算最短路径树,首先distTo[s]设置为0,数组中其他元素设置为正无穷,然后依次放松
为了保证可以实现依次放松,引入了一条索引优先队列pq,用来保存需要被放松的顶点和下一个要放松的顶点
具体的操作如下
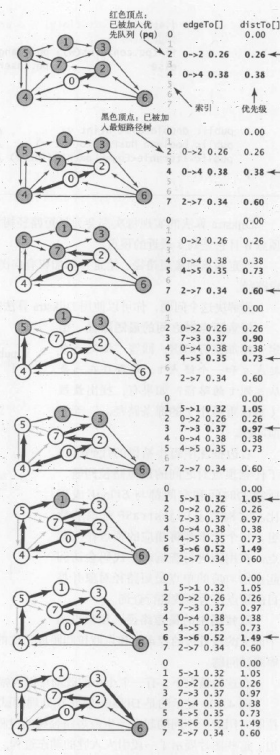

上面可以看出来算法的运算过程
可以把他和Prim算法进行对比,都是属于通过添加边的形式添加树,
只不过Dijkstra算法每次添加离起点最近的非树顶点到树的边
核心的操作就是
从优先队列U中选出”距离最短的顶点k”,并将顶点k加入到优先队列S中;同时,从U中移除顶点k。
更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
接下来,我们引入一个可以在线性时间内解决的加权无环图中的最短路径算法
且考虑负权重的有向图的的最短路径问题
本次介绍的算法具有的特点为:
能够在线性时间内解决单点最短路径的问题
能够处理负权重的边
能够考虑找出最长的路径等类的问题
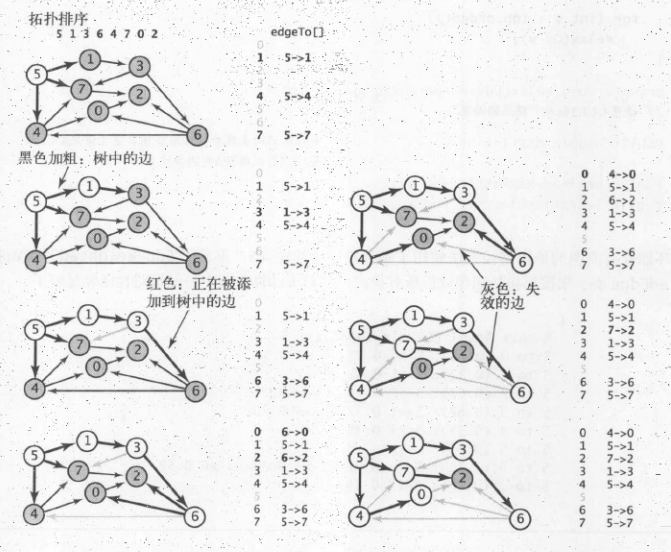

简单来说这个算法就是讲松弛和深度优先结合起来
最终寻找到一个最小生成树