如何去查看拜占庭将军问题,其实是借助拜占庭将军的故事展示了分布式共识问题,是分布式领域比较困难的一个容错模型,一旦搞懂了,就可以掌握分布式共识的解决思路
接下来我们来看看这个算法
我们假设利用六国抗秦的故事来讲述这个问题
假设,战国时期,六国需要联合抗秦,这就需要进行统一的战斗准备
万一其中有人是叛徒,在发送一些不利的消息,导致,自己的计划被打乱了,那么怎么办呢?
归根结底,就说要保证统一的计划制定,这就类似拜占庭将军问题
如何利用合适的通讯方式,来讲多个将军大成共识,制定一致性的作战计划
首先是一个场景
有两个同伙一个叛徒的问题
假设有三个国家
齐楚燕,我们需要保证同伙间的一致性,来从而保证能够去对抗秦国,也就是要保证能做到少数服从多数
那么如果进行实例化,就是如下的表现方式
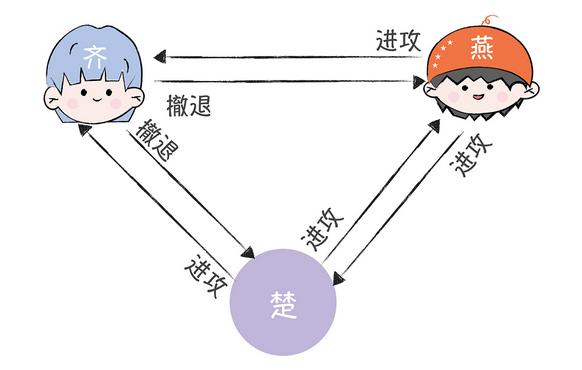
楚燕表示进攻,那么齐国就得服从
但是如果楚国是个叛徒,导致了作战计划不一致,比如,如下的发送方式
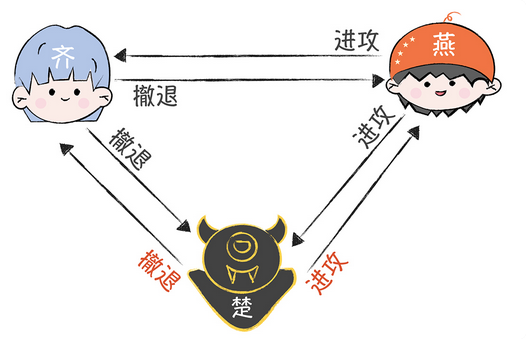
导致齐国看到的是 撤退大于进攻
燕国看到的是,进攻大于撤退
那么就是经典的二忠一叛问题,如何解决呢?
第一种方式是
口信型解决方案
就是由苏秦亲自加入讨论,从三位将军变为四位将军的讨论,增加了忠诚的将军数量
那么我们还需要加入一些流程来保证安全性,比如加入了两轮的讨论
第一轮:先发送消息的做指挥官,其他做副官
然后副官收到指令后,将其作为自己的指令
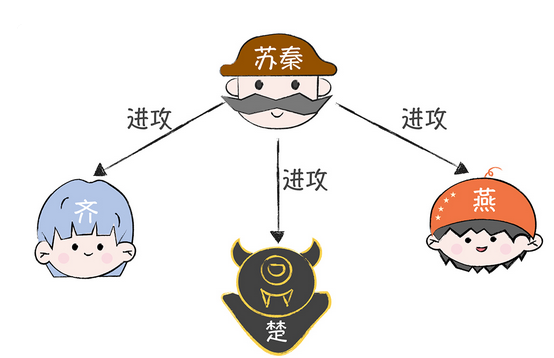
第二轮:剩下3位副官,变为指挥官,向其余2位发送作战指令
然后按照少数服从多数,执行作战指令
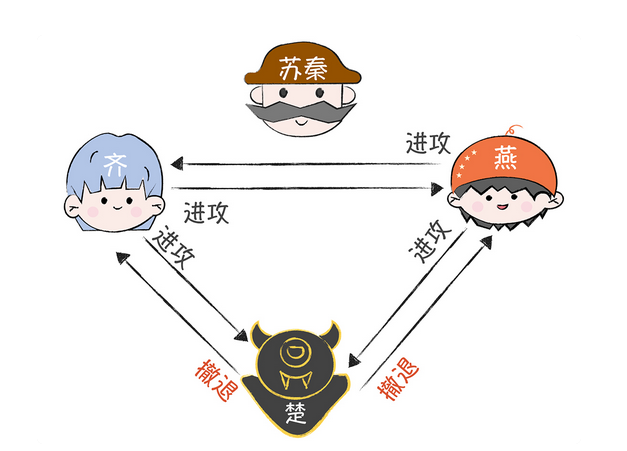
在这一轮,楚国没有发送进攻,而是发送了撤退,即时这样,那么齐 燕收到的信息是 进攻 进攻 撤退,这样也能保证作战的一致性,保证了作战的胜利
如果是楚国先发的消息,那么也会变成这样的情况
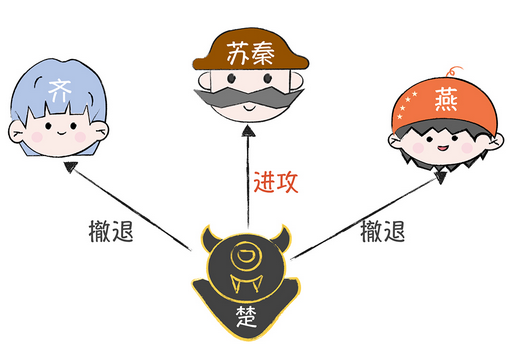
分别发送了撤退 进攻 撤退
那么在第二轮的发送中
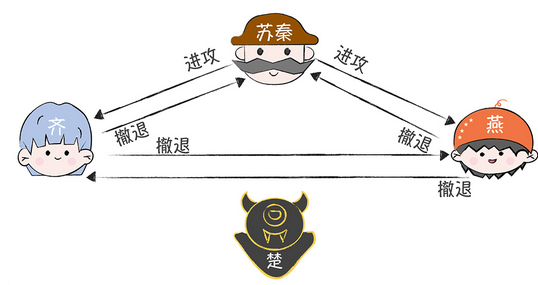
也会产生如下的情况,
导致最后收到的是 撤退撤退 进攻,保证了作战的一致性,这样,无论如何捣乱,都能有一致的计划
这就是经典的拜占庭问题的,如果叛徒的数量是m,那么同伙人数不能小于3m+1,那么就可以解决了
同理反推
如果有m个叛徒,那么会决定递归循环的次数,即为m+1轮,可以从另外的角度理解,n个人,最多能容忍(n-1)/3位叛徒
这个解决方案比较弱的地方在于,将军人数必须增加,如果不能增加的话,有什么解决方案吗?
那就是第二种解决的方案
就是通关不可变的签名的方式,进行相对应的设计
假设,一个人的签名无法被伪造,且如果有修改,立刻能被发现,那么流程可能是这样
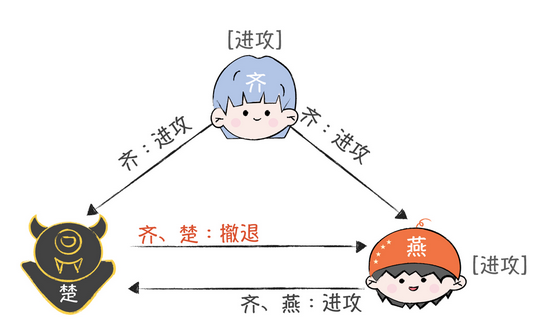
齐国发起进攻指令,那么楚国收到后进行了串改,到了燕手上,燕发现是假的,于是会忽略楚的作战信息,执行齐的进攻命令
如果是楚先发送的作战信息
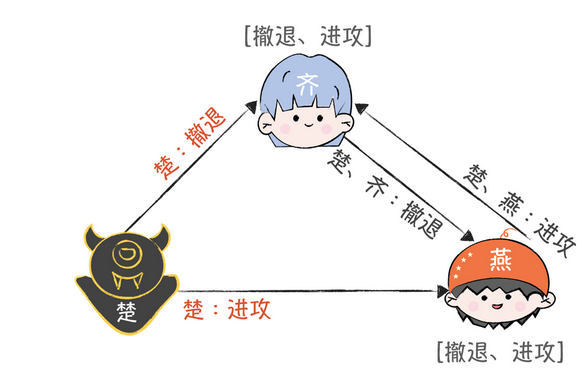
这样,看似破坏了三者的平衡,那么剩下两者都是收到了进攻和撤退的信息,那就只好根据一些特定的设置好的规则,来保证一致性了
这个问题,就是签名消息型拜占庭问题之解,这样就能在某种意义上一直保证一致性
对应上面的拜占庭,我们在计算机的世界中
1.故事中的各位将军,可以认为是计算机节点
2.同伙,就是正常节点
3,叛徒,就是故障的且会发送误导信息的节点
4.信使死亡,就是网络不通,信息丢失
5.被人伪造签名,就是恶意劫持
这样,那么这种故障行为,是带有恶意行为的,所以,在可能存在恶意节点的行为中,必须使用拜占庭容错算法,除了这两种拜占庭容错算法,还有着PFBT算法,PoW算法
而且,还有很多非拜占庭容错的算法,故障容错算法,既CFT算法,解决的是分布式系统汇总存在故障,但没有恶意节点的共识问题,常见有Paxos, Raft ZAB协议
根据合适的场景选择合适的算法,如果节点是可信的,不存在篡改的问题,使用非拜占庭算法,反之拜占庭算法比较合适
课后思考
拜占庭容错算法和非拜占庭容错算法,分别适合那些场景呢?
对于一些传统的,部署在私有云或者VPC的场景,一般会使用非拜占庭算法
对于一些部署在公网的集群,且在集群中可能存在恶意攻击的人,例如涉及金融的类银行网络,使用拜占庭算法比较好