基础数学课11-概率
我们接下来来了解下,概率和统计的相关信息
首先是在概率和统计中需要掌握的概念,
对于概率来说,往往在现实世界中,发生事件的概率是不一定的。如果我们对一个数组执行查找操作。如果需要从头到尾全部搜索一边,那么其平均扫描次数是(n + 1)/2
但是往往在现实生活中,搜索往往具有倾向性,也就是某几个下标的元素的访问次数远比其他的要多。这就意味着概率分布是不均匀的,最终影响到平均复杂度的加权平均计算。
进一步,到机器学习领域的话,统计和概率的运用更加显而易见。我们需要根据统计的来的数据对机器进行训练,得到模型,最终根据模型来预测数据。
通过概率总结模型,通过样本预测数据,这就是机器学习领域的基础,只不过在此之中,我们会了解到贝叶斯定理。并进行计算简化,从而将繁杂的数据映射到机器学习之中。
对于概率,其描述了一种事件在现实事件中发生的概率。相关的名词包括
随机变量,可以描述事件所有可能发生时的状态,
概率分布,来描述不同状态出现的可能性,
在随机变量之中,分为了离散型随机变量和连续型随机变量
如果可以直接求和得到结果的,就是离散的,如果需要积分进行计算的,就是连续的
这样说有点抽象,我们拿示例一个个的看,最简单的,查看概率分布,我们可以拿抛硬币事件来看。出现正面和反面的概率都是50%,那么正反对应的概率就是0.5,这就是简单的概率分布。
同样这种,直接可以根据公式推断出的值就是离散型随机变量。
对于连续性的随机变量来说,如何理解概率变化呢?
这里我们以一辆汽车在单位内时间的速度变化来进行举例,如果计算在60min内,每一分钟车辆所具有的速度。那么我们可能会得到一个如下的直方图
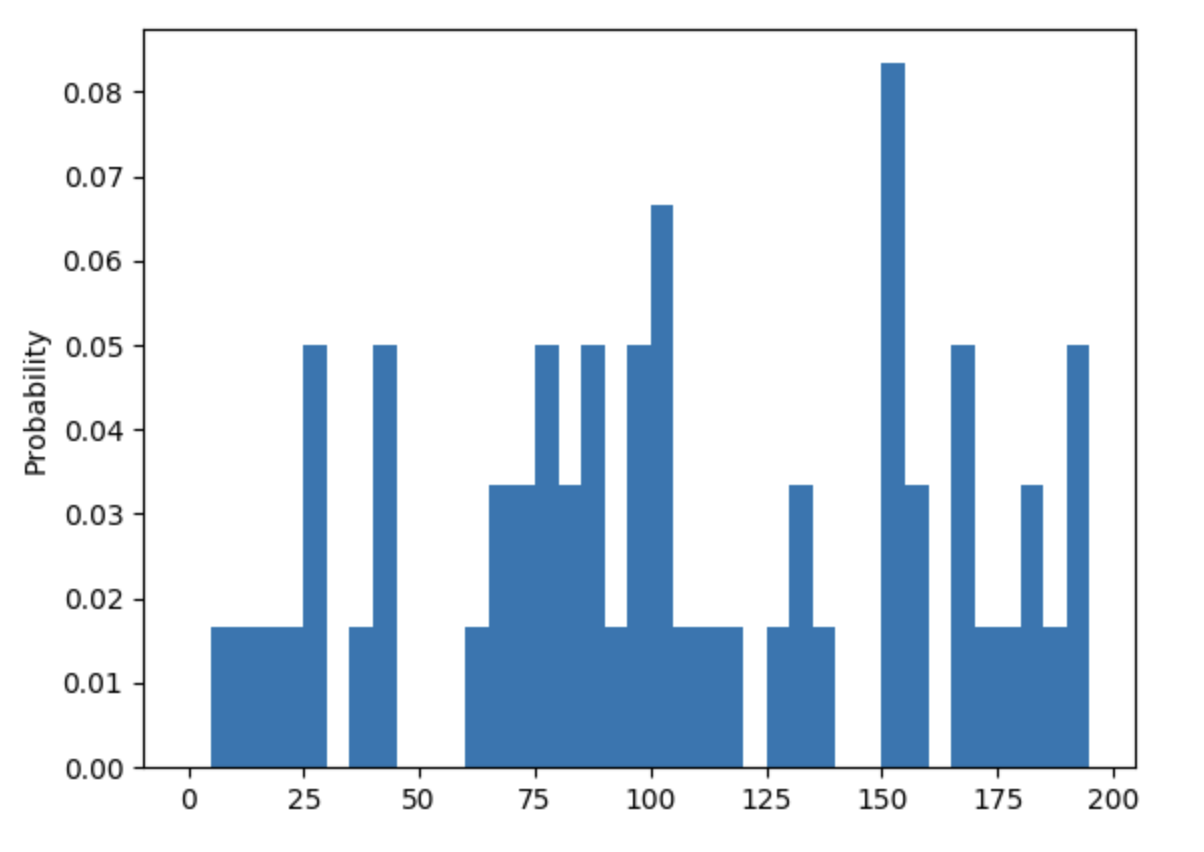
如果时间精度不断调大,同时速度准头不断变高,那么我们最终会得到一个如下的折线图。
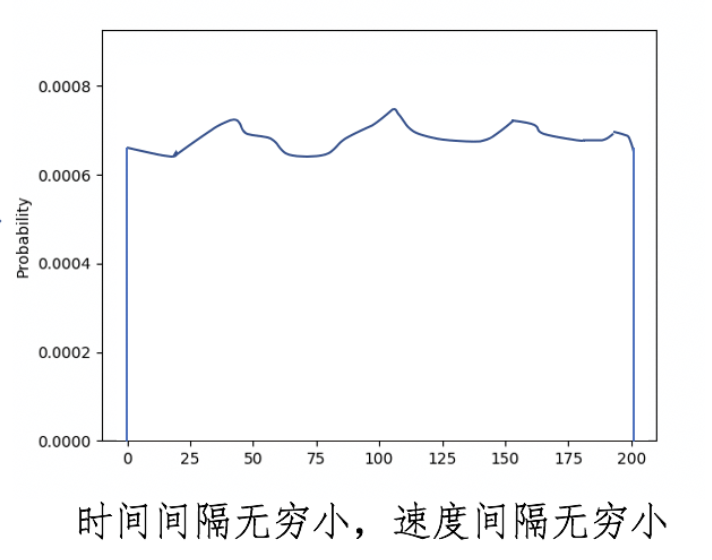
这就是连续分布模型。
对于离散分布模型中,我们来举一些例子,比如伯努利分布,分类分布,二项分布。
伯努利分布,就是单个随机变量的分布,取值只有0和1
就比如上面说的硬币正反面。
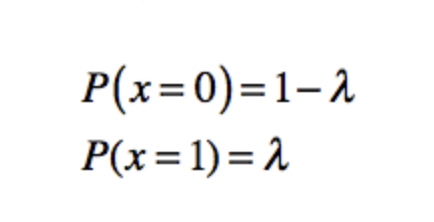
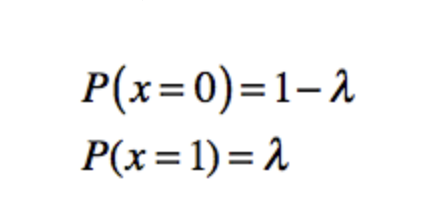
分类分布,则是描述k个不同状态的单个随机变量。这里的k是个有限的数值,如果k为2,那么就是一个简单的伯努利分布。
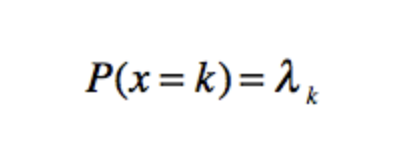
而对于连续性分布来说,模型就比较多了,包含正态分布,均匀分布,指数分布,拉普拉斯分布等。
正态分布的公式如下
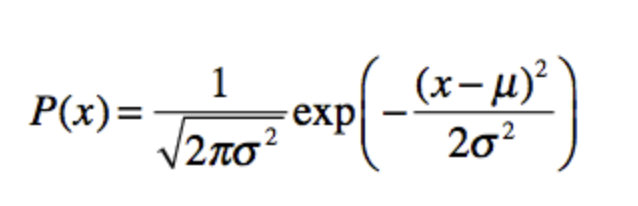
在正态分布模型之中,其概念就是有一个中心点,越距离中心点进,出现的概率越高,反之则降低,最终形成一个如下的图。
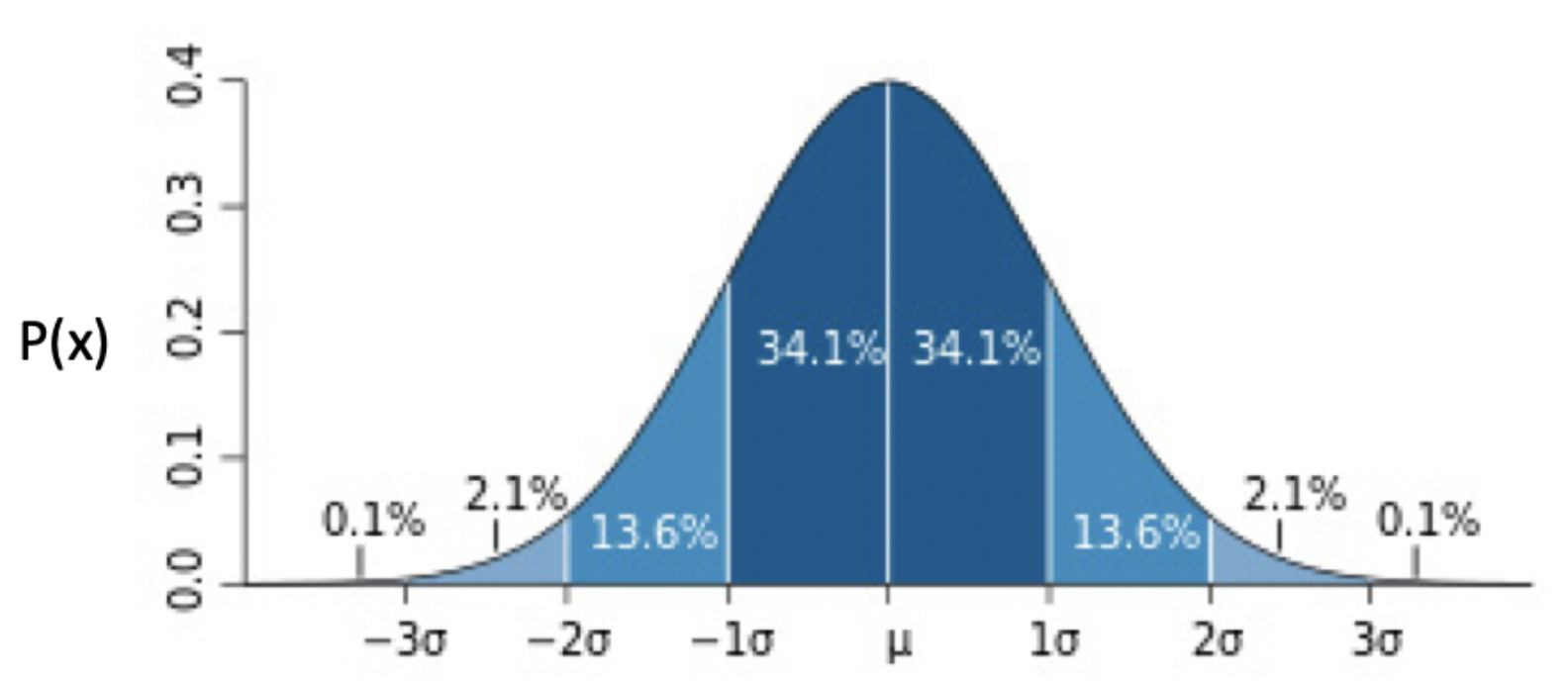
就比如人类的身高分布,大部分的人的身高都是接近平均值的,偏离平均值的身高对应的人,必然较少。
除此外,还有个期望值的概念。也就是数学期望, 就是结果的出现概率乘以其结果的总和。
如果说结果出现的概率是权重,那么期望值就是加权平均值。
在实际应用中,期望值常用于解决一些特定的实际问题,诸如在同一个问题中存在不同的情况
且不同的情
况具有实际的数值,且数值有意义。
就比如来说,我们假设汽车的平均速度。
如果在某一分钟内,汽车的平均速度是5km每小时,下一分钟是40km每小时
那么就符合具有不同的情况,且这些情况可以使用数值来衡量。
那么我们想要获取期望值
就可以先获取1小时行驶的总距离,即每种速度乘以以这个速度形式的时间之和。
之后除以60
得到一个平均值,那么这个平均值,就是对应的期望值。
这就是离散变量的期望值,如果是连续型的期望值,那么需要换一个公式。
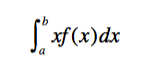
我们还可以延伸出一些概率中的概念
联合概率,条件概率,边缘概率。
假如我们有一份成绩单
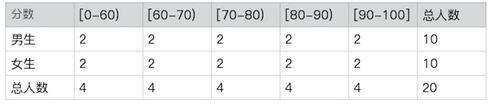
那么我们统计的维度有很多种,简单点的,可以是这个班中90分以上的学生概率,
或者是这个班上男生的概率。
复杂点的可以是这个班上90分以上的男生。
而这种复杂的,复合的条件由性别和分数两个随机变量同时决定,这种由多个随机变量决定的概率叫做联合概率。其概率的分布就是联合概率分布。在现实生活中,我们可以由此延伸出更多维的联合概率分布。
也就是单一的概率分布是P(x)或者P(y)
联合的则是P(x,y)
联合概率和单个离散变量的概念上,我们可以通过概率P(x,y)在y上进行求和,得到P(x)
这种时候可以称为边缘概率。
除此外还有着条件概率的关系,其就是给定了某个或某几个随机变量的条件下,另一个随机变量出现的概念,称为条件概率分布。表示为P(y|x)
简单来说就是,只在男生这个群体中,90分以上的概率是多少。
这种情况下,得到的结果 2/10即20%
那么我们是否可以得到,联合概率是条件概率和概率的乘积

男生中考了90分及以上的概率为P(90-100 | 男生) = |男生, 90-100| / |男生|,全班中男生的概率为P(男) = |男生| / |全班|。如果我们将p(90-100 | 男生) 乘以 P(男) 会得到什么结果呢?
(|男, 90-100| / |男生|) * (|男生| / |全班|) = |男, 90-100| / |全班|
这种三角关系,就是贝叶斯定理。
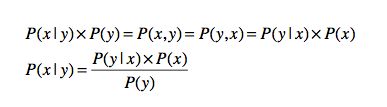
这种定理常用于推算联合概率或者条件概率
其中我们将P(x)称为先验概念,然后P(y|x)是给定x之后y出现的条件概率,除此外,还有边缘概率P(y)
Px主要的来源是数据观测,
Py的主要来源是根据联合概率推测出来。
这样,我们可以根据先验定律推测出后验概率。
最后我们说下变量之间的独立性
对于变量的独立性而言,如果我们可以笃定几个变量具有独立性,那么可以在我们进行概率推测的时候进行简化。
比如我们有5个随机变量,如果直接计算联合概率,那么可能是一个次方级别的取值。
如果进行确定他们之间彼此独立的话,
我们只需要分别计算他们的概率就可以了。
所以在实际的项目,我们可以先假设多个变量之间的独立的,从而帮助简化计算,虽然这一点的假设往往不成立,但是可以帮助我们得到一个近似的解。从而迅速的构建分类器。
最后总结一下,如果我们有一定的标注数据,那么可以通过统计的方法,得到先验概率和似然函数,之后推算后验概率,最后根据后验概率来进行推测。