B树索引是数据库中存取和查找文件(称为记录或键值)的一种方法,应用于磁盘读取方面
B树(B-tree)是一种树状数据结构,它能够存储数据、对其进行排序并允许以O(log n)的时间复杂度运行进行查找、顺序读取、插入和删除的数据结构。B树,概括来说是一个节点可以拥有多于2个子节点的二叉查找树。与自平衡二叉查找树不同,B-树为系统最优化大块数据的读和写操作。B-tree算法减少定位记录时所经历的中间过程,从而加快存取速度。普遍运用在数据库和文件系统。
常见的B树被称为,m阶B树
具有以下性质:
每个点最多有m个孩子
每个非叶子节点(根节点除外)最多有m/2(向上取整)个孩子
root至少有2个子树,除非root的孩子是叶子节点
k个孩子的非叶子节点含有k-1个键值
所有的叶子节点都在同一层,并且内部节点不携带任何信息。(B树的阶指最大子节点数。优势,m阶的b树节点定义为有k个键值和k+1个指针,其中m<=k<=2m,用于指定最少的子节点数)
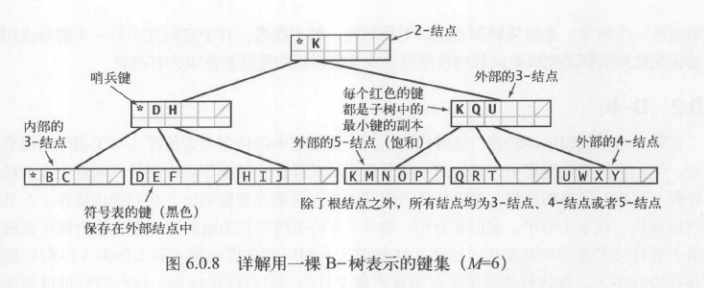
为了实现一个B树,为此使用了一种名为哨兵键的方法
而且引入两种不同类型的结点来做到这一点
内部结点 含有页相关联的键的副本
外部结点 含有指向实际数据的引用
内部结点中的每一个键都和一个子结点相关联,所有的子节点的键都大于等于和此结点关联的键
如何查找
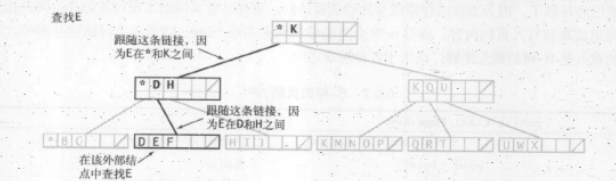
查找就是在被查找的键包含在集合中时,每次查找便会结束在一个外部结点
在内部节点中遇到被查找的键就判断命中并且结束,但是肯定会有包含对应键的外部结点
由上图可以看出来,根据被查找的键所在根节点的不同区间之中,根据结点的区间移动到下一个合适结点
最终查找到了对应的键应该在的结点,如果要查找的键在此结点中,那么查找结束
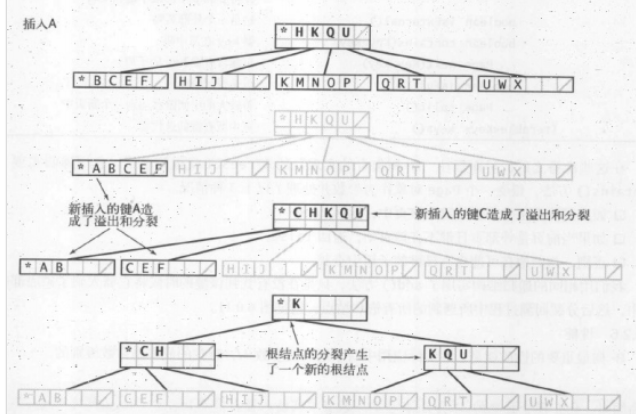
假设一个6阶B树要插入,如果空间允许,则直接插入,如果空间已经满了,则可以允许被插入的结点暂时溢出(变成一个-6结点),但在递归调用向上
之后不断分裂此结点,如果根节点也满了(成为了一个-6结点),那么可以将其分裂成连接两个-3结点的-2结点
然后依次向下,做如此行径 将6结点的父节点-k结点变成 -(k+1)结点
上面的3替换成了M/2结点,6替换成M,就是适用于所有的B树的插入算法
对于B树的实现.可供选择的表达式
定义了一种名为Page的数据结构
并实现了一套配套的API

根据此API就很容易起实现BTree,使用contains()来递归实现查找方法,并接受Page对象作为参数处理三种情况
1 如果当前页为外部页且键在页中,返回true;
2 如果当前页为外部页且键不在页中,返回fasle;
3 递归的在该键的子树中查找

对应的B树还有很多的变种,方便去直接使用,比如B+树
B+树是B树的一个升级版,相对于B树来说B+树更充分的利用了节点的空间,让查询速度更加稳定,其速度完全接近于二分法查找。为什么说B+树查找的效率要比B树更高、更稳定;我们先看看两者的区别
(1)B+跟B树不同B+树的非叶子节点不保存关键字记录的指针,只进行数据索引,这样使得B+树每个非叶子节点所能保存的关键字大大增加;
(2)B+树叶子节点保存了父节点的所有关键字记录的指针,所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样;
(3)B+树叶子节点的关键字从小到大有序排列,左边结尾数据都会保存右边节点开始数据的指针。
(4)非叶子节点的子节点数=关键字数(来源百度百科)(根据各种资料 这里有两种算法的实现方式,另一种为非叶节点的关键字数=子节点数-1(来源维基百科),虽然他们数据排列结构不一样,但其原理还是一样的Mysql 的B+树是用第一种方式实现);
具体的实现就不给出了
但MySQL就是使用B+树实现的数据存储
