放弃原有的二进制来表示一个字符,而是采用了较少的比特来表示出现频率高的字符,用较多的比特表示出现频率低的字符
如果需要对 ABRACADABRA!来编码的话,简单且直接的运算就是转换成二进制,但是这样出现频率最高的A和只出现一次的!所占的空间相同,出现无法识别的问题
不如,将A编码为0,B编码为1,R为00,C为01,D为10,!为11.
虽然不完整,但是可以初步的体现我们的压缩思想
为了完善这个思想,引入了前缀码这个概念
但是,0可以误解为R,C,D
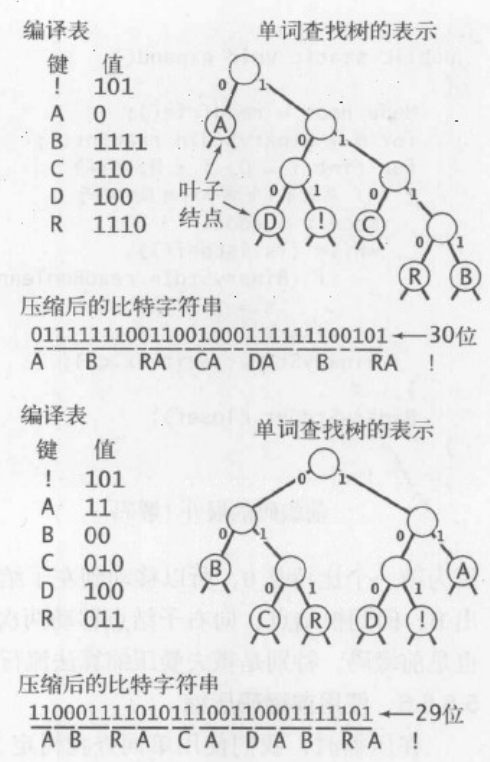
但如果我们将A编码为0,B为1111,C为110,D为100 ,R为1110 ,!为101
那么就不会出现误解这个可能性了
前缀码可以用来形成一个单词查找树
只利用叶子节点来表示字符,但中间节点并不是没有含义
简单来说,就是形成一个从根节点到该节点的路径表示的比特字符串,左为0,右为1的树
那么,最后的最优的且最经典的树构建方法被称为霍夫曼编码
利用前缀码进行数据压缩需要经过5个步骤
构造一颗编码单词查找树
将该树以字节流的形式写入输入以供展开使用
使用该树将字节流编码为比特流
读取单词查找树
使用该树将比特流解码
树的结点并不难,只是简单的使用了类似链表的内部类结构,含有分别指向左和右两个结点的Node
private static class Node implements Comparable<Node>
{
private char ch;
private int freq;
private final Node left,right;
}
对应的,如果需要展开整个树,则需要
调用一个从标准输入获取数字的的方法,然后根据比特流的输入从根节点开始移动,如果为0移动向左子节点,如果为1移动向右子节点.直到寻到一个根节点

如果需要对前缀码进行压缩

维护一个String数组st,然后buildCode遍历查找树中对应字节
对于任意的单词查找树,都能够产生一个将树中的字符和比特字符串相对应的编译表
那么困难就是,对于单词查找树的初次构造
我们先维护创建一个由许多只有一个结点的树组成的森林,
每个结点的Node中我们维护了一个freq的实例变量来表示出现的频率
为了得到正确的频率,需要读取整个输入流,故霍夫曼算法是一个两轮算法
不断的寻找两个频率最小的结点,然后创建一个二者为子节点的新节点(新节点的频率为两个子节点的频率之和)
private static Node buildTrie(int[] freq) {//获取频率
MinPQ<Node> pq = new MinPQ<Node>();
for (char c = 0; c < R; c++) {
if (freq[c] > 0){
pq.insert(new Node(c, freq[c], null, null));//遍历插入
}
}
while ((pq.size()) > 1) {
Node x = pq.delMin();
Node y = pq.delMin();
Node parent = new Node(‘\0’, x.freq + y.freq, x, y);
pq.insert(parent);
}
return pq.delMin();
}
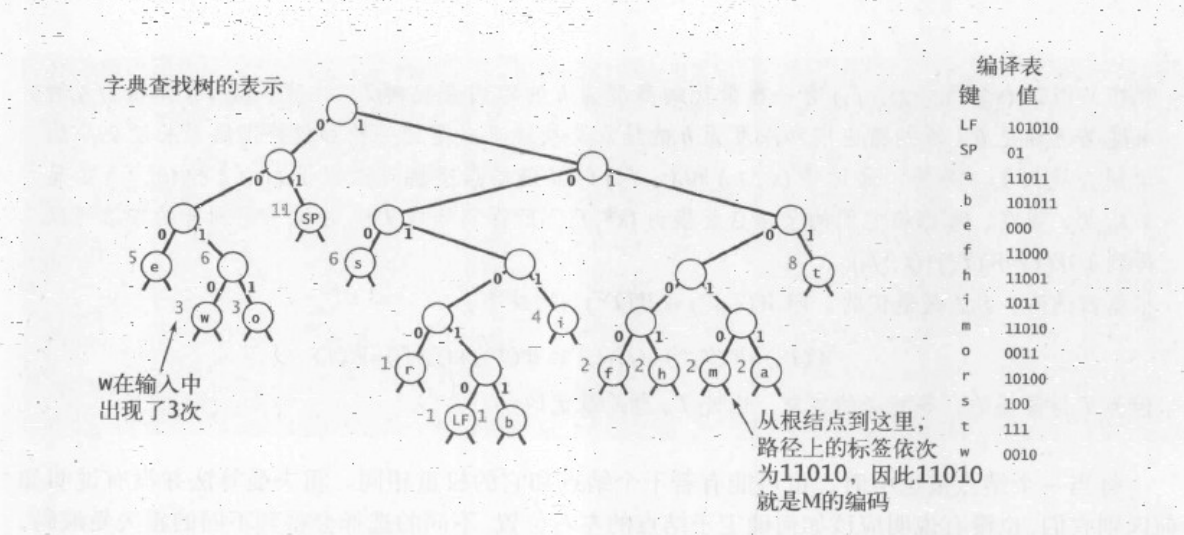
构成了一个字典查找树
这样配合上面的写入,就可以进行写入到输出流了
下一步就是压缩
我们对于单词树的约定压缩和解析格式
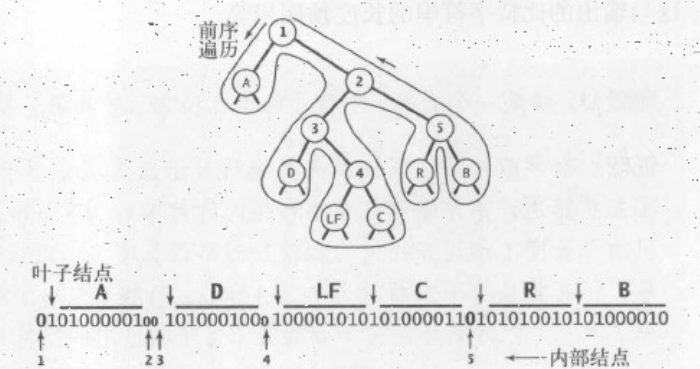
对整个单词查找树进行前序遍历,
如果找到了一个内部节点,则写入一个0,如果是一个叶子结点,则写入一个1,然后写入对应字符的8位ASCII码
其遍历方式按照如此,读取一个比特来获取当前节点的类型,如果是0则为内部节点并继续构造他的左右子树
如果是1则构造一个叶子结点就读取字符编码并且构造一个叶子结点
private static void writeTrie(Node x) {
if (x.isLeaf) {
BinaryStdOut.write(true);
BinaryStdOut.write(x.ch);//写入字符串
return;
}
BinaryStdOut.write(false)
writeTrie(x.left);
writeTrie(x.right);
}
总结下来:
压缩的实现顺序为
读取输入;
将输入的每个char值的出现频率制作成表格
根据频率构造相对应的霍夫曼编码树
构造编译表,将输入的每一个char值和一个比特字符串相关联
将单词查找树编码为比特字符串并写入输出流
将单词总数编码为比特字符串并写入输出流
使用编译表来编译每一个字符,并写入输出流
展开顺序为:…
读取单词查找树
读取要解码的字符数量
使用单词查找树将比特流进行解码