字符串的查找一种即为子字符串查找,给定一个长度为N的文本和长度为M的模式字符串
然后利用模式字符串去匹配文本
常见的方式有
第一种,暴力子字符串查找算法
使用一个指针追踪文本,另一个追踪模式,对于每个文本键值,我们都重新循环遍历模式,如果发现不重合的字符,就终止本次循环
直到发现全重合的位置
其算法的优点再与比较次数极小,因为大部分的字符第一个就不匹配,
但是如果模式字符串拥有一大串的相同字符,那么可能会极慢
所以在二进制中,这种方法并不合适
然后根据暴力子字符串查找之后
引入了Knuth-Morris-Pratt算法(KMP算法)
在此基础上,在查找过程中,记录可能会接下来可能用到的位置
当发现不匹配的键时候,不必退回到开始,而是在已经遍历过的中匹配,这样一共只需要N次比较
利用之前已经部分匹配的有效信息,保证i指针不回溯,通过修改i指针,让模拟串尽量向前移动
其算法的核心在于模式指针的回退
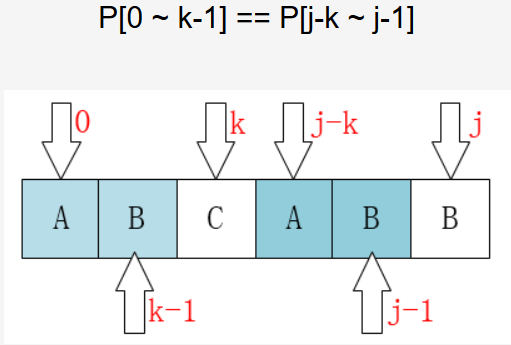

由上面的公式可以推断出,j要移动到k的位置,有一个重要的性质:
最前面的k个字符和j之前的最后k个字符是一样的
所以,我们可以使用一个数组来保存,next[j] = k,当需要的时候,就把j移到k
public static int[] getNext(String ps) {
char[] p = ps.toCharArray();
int[] next = new int[p.length];
next[0] = -1;
int j = 0;
int k = -1;
while (j < p.length – 1) {
if (k == -1 || p[j] == p[k]) {
next[++j] = ++k;
} else {
k = next[k];
}
}
return next;
}
不过在这里,我们使用的是DFA(有限状态自动机)来解决的
那么API应该很简单

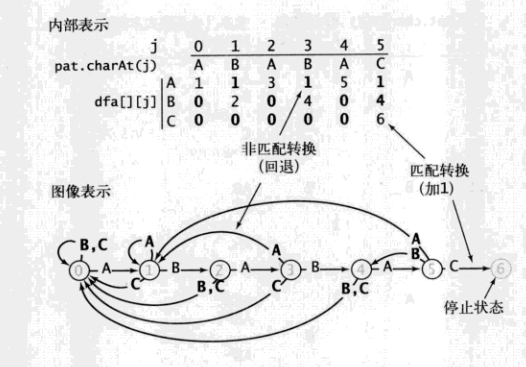
自动机是由状态和转换组成的,状态是由圆圈,转换是由箭头表示的
只有满足了条件,箭头才会向右走
如果走到了模式的长度M,那么就认为找到了
这样就只需要模式完整的走一遍就能完成查找
接下来构造DFA
我们并不想重新扫描一遍已知的文本,只需要知道如何DFA重置到合适的位置
我们需要在处理dfa[][]的第j列时维护重启位置x
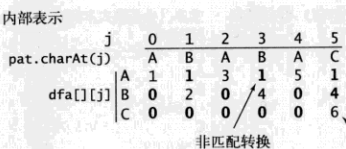
dfa[txt.charAt(i)][j] -> dfa[a][0] =1;
代码的梳理为
在创建DFA的时候
for (int X = 0, j = 1; j < M; j++) {
for (int c = 0; c < R; c++) {
dfa[c][j] = dfa[c][X];// 失败情况下的方法
}
dfa[pat.charAt(j)][j] = j + 1;
/*
* 因为自动机是为了让 s[j+1] = dfa[(txt.charAt(i)][j]; 且相同有 dfa[(txt.charAt(j)][j] = j+1;
*
*/
X = dfa[pat.charAt(j)][X];// 更新
}
上面的代码,简述为
对于每个j,
匹配失败的时候,dfa[][X]复制到dfa[][j];
匹配成功的时候,dfa[pat.charAt(j)][j]设置为j+1;
更新X。
public int search(String txt) {
int i, j;
int N = txt.length();
int M = pat.length();
for (i = 0, j = 0; i < N && j < M; i++) {
j = dfa[txt.charAt(i)][j];
}
if (j==M) {
return i-M;
}else {
return -1;
}
}
search则相对简单
public int search(String txt) {
int i, j;
int N = txt.length();
int M = pat.length();
for (i = 0, j = 0; i < N && j < M; i++) {
j = dfa[txt.charAt(i)][j];
}
if (j==M) {
return i-M;
}else {
return -1;
}
}
最后,总结一下KMP的性能特点
适合查找具有多个重复的字符的字符串
KMP为最坏情况提供了线性级别的运行时间保证,
虽然在时机运算中,比暴力算法的优势并不明显
接下来,学习一种大量利用回退的算法
然后是Boyer-Moore字符串查找算法
BM的查找方式,和KMP的类似但是,相对来说简单
同样也需要一个记录位置的数组,根据匹配失败时候文本和模式来决定下一步的行动

利用一个从右往左匹配的数组,
其匹配流程如下,查找NEEDLE
首先查找第五位,发现不是E,但是是N,直接跳转到5,然后匹配第10位,发现第10位不在数组中,直接右移6位,然后匹配16位,发现为E,但是其左侧的字符为N,左侧匹配失败,
右移5位,进行匹配
具体实现细节:
1.使用数组right[]记录字母表每个字符在模式出现的最靠右的地方,我们应该最小跳跃多少
首先将right[]数组初始化,设为-1,然后对于在0到M-1的j,将right[pat.charAt(j)]设为j
2.再检查过程中,如果j检查完了0到了M-1的字符,就相当于找到了匹配,不然匹配失败,会进入下列情况.
如果发现失败的字符不包含在模式字符串之中,使模式字符串向右移动j+1位,
如果发现失败的字符在模式字符串中,使用right[]数组来让模式字符串和文本对齐,
最后是Rabin-Karp指纹字符串查找算法
基于散列的字符串查找算法,需要计算模式字符串的散列函数,然后依次比对
基本实现为:
长度为M的字符串对应R进制的M位数,所以需要一个能够转化的int值散列函数,(可以借用除留余数法)
然后依次比对
比如查找3145467626535中的26535,那么可以先进行散列,使用散列表,26535%997 = 613
然后依次比较 字符串中的5个键的散列值,31454的hash值 14546的hash值等
直到发现了匹配的模式字符串hash值

方法不错,重点在于,散列函数的计算方式

对于每一个数字,都将散列值乘以R,加上这个数字本身,除以Q(散列表大小)
使用这个方法的成本就是对文本中每个字符进行乘法和加法取余成本计算之和
最坏情况下需要NM次操作
Rabin-Karp被称为指纹字符串查找算法,因为他只用了极少量的信息就表示了
算法的高效来源于对指纹的计算和比较
最后,对于各种子字符串查找算法
暴力查找算法简单而且在一般情况下都工作良好
Knuth-Morris-Pratt算法能够保证线性级别的性能且不回退
Boyer-Moore算法的性能一般都是亚线性的
Rabin-Karp算法的线性级别,MN成正比
Knuth-Morris-Pratt和Boyer-Moore算法都需要额外的内存,Rabin-Karp的内循环很长