简单来说,仅仅是一个边和两个顶点之间的连接

这份API包含两个构造函数,分别接受一个整数,并常见一个包含整数个数的图
第二个构造函数,接受输入由2e+1个整数组成,显示V,E,然后E对 V-1之间的整数
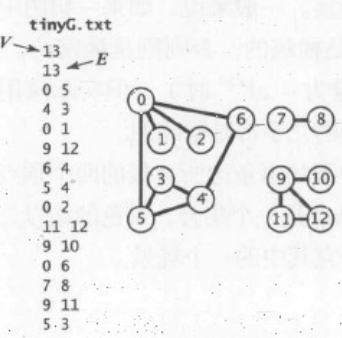
前两个分别代表了,V和E,构成如上的图
图的实现可以考虑如下的几种方式
1.邻接矩阵:使用一个V乘以V的布尔矩阵,当顶点v和顶点w之间有相连接的边时,定义v行w列的元素为true
但是其占用空间过大,无法满足
2.边的数组:使用一个Edge类,含有两个int实例变量,但是这种方式实在不符合adj的方法实现,如果这样写,每次查找都会遍历一边图
3.邻接表数组:一个以顶点为索引的列表数组,其中每个元素都是和顶点相邻的顶点列表,这是最符合的
实现如下
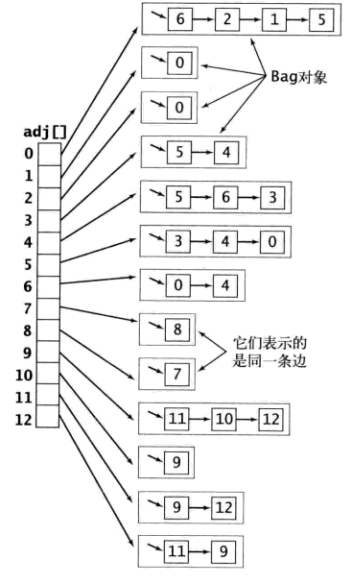
使用多维数组实现如上的方式进行测试
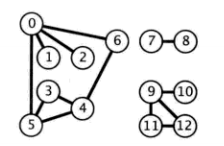
每个顶点后的相邻表,可以使用集合实现
对应的添加一条边,是在在V-W之间添加一个边,会在V的相邻表中添加W,W的相邻表中添加V
其性能特点:
使用的空间和V+E成正比
添加一条边的时间控制在常数呢
遍历顶点V的所有相邻顶点和所需的时间和V的度数成正比(处理每个相邻顶点时间皆为常数)
但仍需要注意,插入顺序决定了在表中的出现顺序,故要严格保证出现顺序
public Graph(int V) {
this.V = V;//赋值过去
this.E = 0;
adj = (Bag2<Integer>[]) new Bag2[V]; //创建一个链表
for (int i = 0; i < adj.length; i++) {
adj[i] = new Bag2<Integer>();
}
}
public Graph(InputStream input) throws IOException {
this(input.read());
int E = input.read();//读取
for (int i = 0; i < E; i++) {
int v = input.read();
int w = input.read();
addEdge(v, w);
}
}
public void addEdge(int v, int w) {
adj[v].add(w);
adj[w].add(v);//相互添加
E++;
}
这两个构造方法分别利用图和整形来创建图
这里面每插入一对v-w顶点,都会插入两次
还有其他的操作也很常见,添加一个顶点和删除一个顶点
这样的简单实现的可能性为使用符号表来代替数组
之后在进行扩展API
删除一条边,检查图中是否含有边V-W
实现了基本的图,我们来看下常见的无向图API如下

然后关于无环图,还有一个顺序的搜索每一个边
如何避免可能会出现的重复搜索

搜索相关的API如下

对于这个搜索,我们需要引入递归这个概念
简单来说就是,在访问一个结点的时候,把这个节点标记为已经访问
递归的访问没访问的邻居结点
比如深度优先遍历
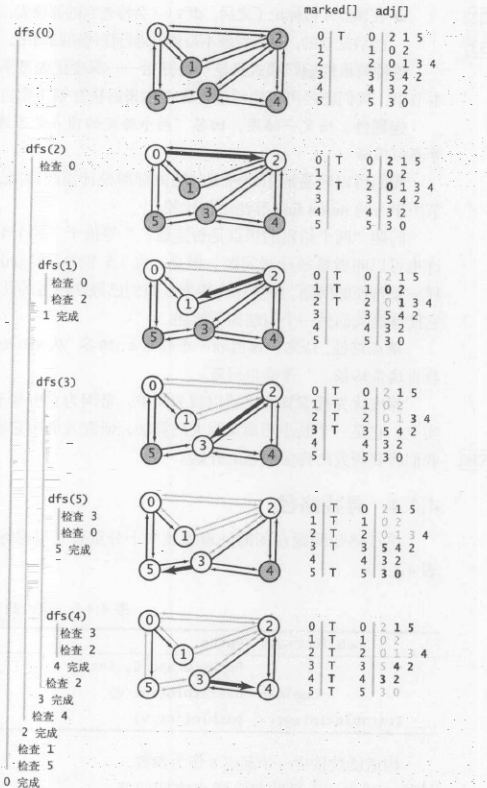
利用递归的方法,依次查找,如果邻接表内都已经被标记了,返回上一层,进行下一个,依次直到没有没被标记的
利用这种递归,我们能够解决很多有效的处理很多和图相关的任务
例如:
两个给定的顶点是否连通,图中还有多少个连通子图
或者给定一个起点s,从s到给定目的顶点v之间是否存在一个路径

其次是广度遍历优先
深度优先类似一个人在迷宫之中进行探索,而广度优先就像一个探索队,遇到一个岔路,就分成两个
然后再岔路后相遇,就合并
在深度遍历之中,我们调用了一个下压栈,使用后进先出的规则来描述
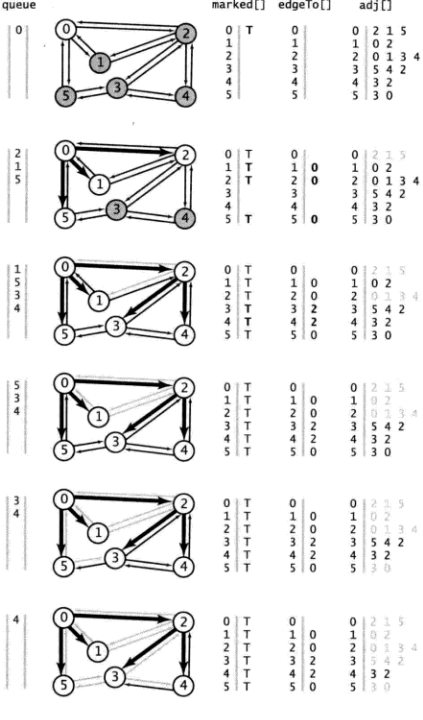
在广度遍历之中,我们使用了队列即可,选择最早遇到的那条
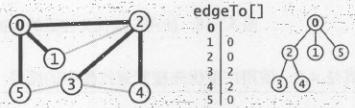
我们先把0加入进去队列
然后把删除0把他的相邻结点 2 1 5 加入进去,把这几个的结点edgeTo[]的值设置为0
然后删除 2 ,把他的相邻结点,把 1 5 3 4 加进去,但是 1 5 已经标记了,所以我们只能把 3 4结点edgeTo[]设置为1
剩下的按顺序添加,然后按顺序检查是否标记了,然后依次删除
最后的最后,我们看一下几个实现的特殊功能
比如查找一个图中有多少个连通树

实现思路:
获取一个图,然后按照图的顺序,先读取按照索引,深度遍历其连通的顶点,给每个顶点都做上相同的标记.查询完成(没有再连通的),循环进行下一个查找,如果没有被遍历,就说明是新的连通树
在进行深度遍历,给其上每个顶点都做上相同标记
