对于图,应用面积极其的广泛

我们在本章的学习中,将图分为
无向图(简单连接) 有向图(连接有方向性) 加权图(连接带权值) 加权有向图(既有方向又带权值)
对于图,基本概念是
一组顶点和一组能够将两个顶点相连的边组成的.
顶点本身叫什么不重要,需要一个方法来指代这些顶点,故常用0-(V-1)来表示一个含有V的顶点的图
可以使用数组的索引来直接作为结点名称
使用符号表也行,两者效率无大区别
并使用 V-W的记法来表示连接V-W的边.W-V则是另一种表示方法
图中有些特殊的概念
1.子环:即一条连接一个顶点和自身的边
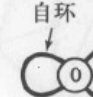
2.平行边:连接同一对顶点的两条边叫平行边
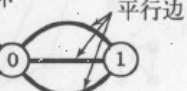
3.相邻:两个顶点通过一个边连接时候,称这两个顶点为相邻,并称这个连接依附于这两个顶点
4.子图:一幅图的所有边的一个子集(以及所依附的所有顶点)
5.路径:是由边顺序连接的一系列顶点,简单路径是一条没有重复顶点的路径
6.环:是一条至少含有一条边且起点和终点相同的路径
7.简单环是一条不含重复顶点和边的环,路径或者环的长度为其中包含的边数
8.如果从任意一个结点都存在一条路径可以达到另一个任意顶点,我们就称这个图为连通图
9.当两个顶点之间存在一条连接双方的路径,称一个顶点和另一个是连通的
10.无环图
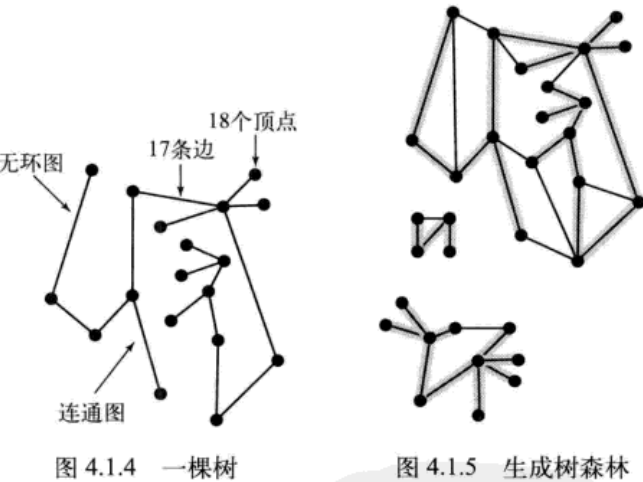
11.树:一个含有V个节点的图G,含有以下5个条件,他就是一棵树

最后,在面对一个有向图的路径问题时候,需要思考有向图的性质,是否含有有权重的边,是否含有环,是否含有有负重的环?
对应的仓库地址如下