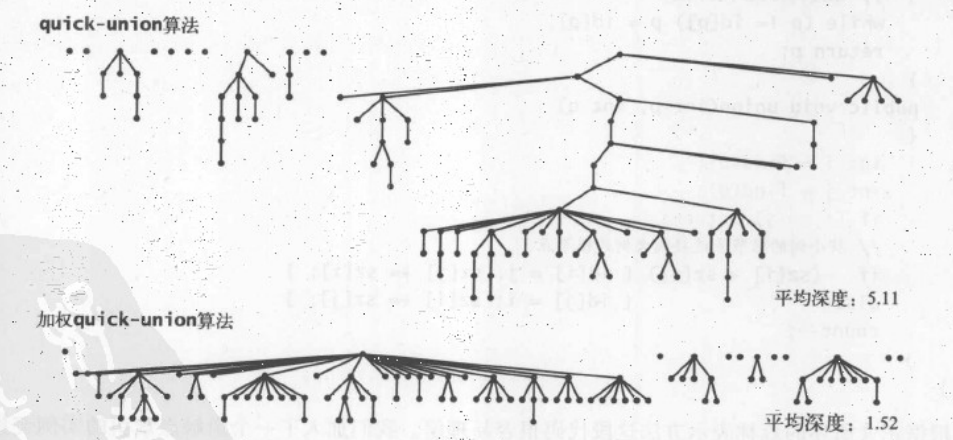
我们先来看一个模型图

主要作用是在一堆数据集合中找到两个触点是否被链接在一起,如果不在一起将这两个点链接在一起,并且最后得出这种链接关系一共有多少个。
每个点都被称为一个触点,,每一个联系称为边,等价类称为连通分量
api如下

我们首先给出一个实现
|
package UF;
/** * * @author Heaven * 此方法为了研究触点问题,并开发出一套行之有效的API *这里我们把触点问题简化成int数据类型的问题; *此方法缺点:每次加连接都需要遍历 *Tip:触点问题类似病毒式扩散,碰到即赋值,大型问题直接GG */ public class UF { private int [] id; private int count;//剩余分量的数量 public UF(int N) { id = new int [N];//创建一个数组格式来存储触点 count = N; for (int i = 0; i < N; i++) { id[i] = i; } } public int count() {//调查数字 return count; } public boolean connected(int p,int q) {//检测连接 return (find(p)==find(q)); } public int find(int p) { //查询所在标识符 return id[p]; } public void union(int p,int q) {//两者之间添加连接,请先确定两者是否连接 int findP = find(p); int findQ = find(q); if (connected(p, q)) return; for (int i = 0; i < id.length; i++) { if (id[i]==findP) { findQ = id[i]; count–; } } } public static void main(String[] args) {//常见用例 int N = 10;//设置输入 UF uf =new UF(N); int count = uf.count; int p = 3; int q = 8; if (!uf.connected(p, q)) { uf.union(p, q); System.out.println(p+” “+q); } } } |
每次去连接,都是讲q设置为p,意味着连接了,但是这样的连接方式,我们使用的是直接遍历,导致的效率并不高
于是,我们改进了一个版本
|
package UF;
/** * * @author Heaven * 此方法我们进一步优化UF结构 * 采用树的方式,只需要将两个节点的根节点连接即可 */ public class UF_02 { private int [] id; private int count;//剩余分量的数量 public UF_02(int N) { id = new int [N];//创建一个数组格式来存储触点 count = N; for (int i = 0; i < N; i++) { id[i] = i; } } public int count() {//调查数字 return count; } public boolean connected(int p,int q) {//检测连接 return (find(p)==find(q)); } /** * * 在此次我们增加额外的判断,便于进行寻找根节点 */ public int find(int p) { //查询所在标识符 if (p != id[p]) { p = id[p]; } return p; } /** * * 在此次我们增加额外的优化,将两个根节点统一 */ public void union(int p,int q) {//两者之间添加连接,请先确定两者是否连接 int pRoot = find(p); int qRoot = find(q); if (pRoot == qRoot) { return ; }//不然进行赋值 id[pRoot] = qRoot; } public static void main(String[] args) {//常见用例 int N = 10;//设置输入 UF_02 uf =new UF_02(N); int count = uf.count; int p = 3; int q = 8; if (!uf.connected(p, q)) { uf.union(p, q); System.out.println(p+” “+q); } } } |
在进行连接之前,我们先进行查找根节点,然后进行连接
但是这并不是极致,因为我们还需要加权,即永远保证,小的树结构连接大的树结构,能够大大改进算法效率.加权的最坏情况:为所有要被归并的树大小都相同,均含有2的平方n个节点,但即使是这样,我们合并之后树的高度也为 2的(n+1)次方
|
package UF;
/** * * @author Heaven * 此方法我们利用了权重的方法,列出两个数组,一个记录树结构,一个记录树的大小 * 每当新的连接,我们就直接寻找两个触点的根节点,将较小的树根节点连接到大的树根节点里面 */ public class UF_03 { private int[] sz;//记录各树的数量级 private int[] id;//记录各树的索引 private int count; public void WeightedQuickUnionUF(int N) {//创建两个数组 count = N; id = new int [N]; for (int i = 0; i < id.length; i++) { id[i] = i; } sz = new int [N]; for (int i = 0; i < sz.length; i++) { sz[i] = i; } } public int size() { return count; }//返回数量 public boolean connected(int p,int q) { return find(p) == find(q); } private int find(int p) {//注意,这一步我要返回的是根节点 while (p != id[p]) { p = id[p]; } return p; } public void union(int p,int q) { int n = find(p); int m = find(q); if (n == m) return; if (sz[n]>sz[m]) {//如果大于,那么把m贴在n上 id[m] = n; sz[n]+=sz[m]; }else { id[n] = m; sz[m]+=sz[n]; } count–; } } |
无限的将小树依靠在大树上,从而保证对应的效率问题
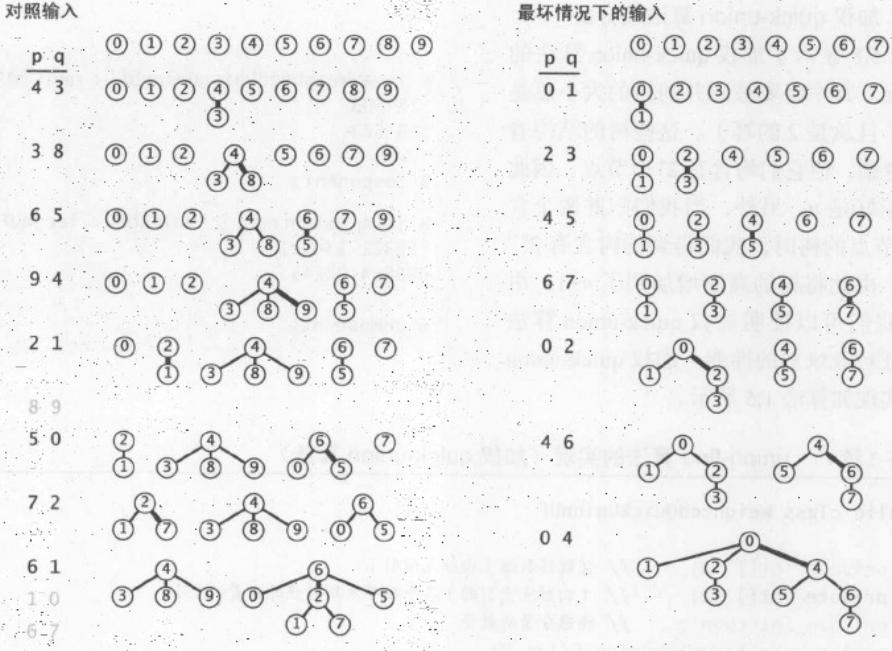
最后两个算法的对比