口信型拜占庭问题的解法是一个非常理论化的算法,因为没有和实际的场景进行结合,
其中还有一个重要的问题,就是对于存在叛徒干扰,可能导致本来想的消息进行相关的变更,从而导致结果和预期相反
那么落地施行的就是PBFT算法,因为口信型拜占庭问题有一个非常致命的缺陷,如果将军的数目为n,叛将数目为f,那么算法需要递归协商 f+1轮,整体的复杂度为 O(n^(f+1)),消息指数级别的暴增
如果叛将数量是64,那么消息总发出数就出超过了int64能够表示的,所以难以落地
PBFT算法很实用,而且在区块链中应用广泛,那现在说一下PBTF算法是如何实现的,还是拿着苏秦抗秦的故事
假设,如下的场景,四个将军之中有一个叛徒,苏秦是客户端,整体的消息都是签名消息,消息无法篡改伪装

如何保证在有叛徒干扰的情况,保证消息的准确无误呢?
我们首先假设苏秦指定的指令是进攻,而楚是叛徒,

首先客户端苏秦联系赵,向着赵发送一个包含作战指令进攻的请求,

当赵收到了苏秦的请求后,会执行三阶段的协议
首先进入准备的阶段,将准备消息进行广播,给与其他的将军这个消息
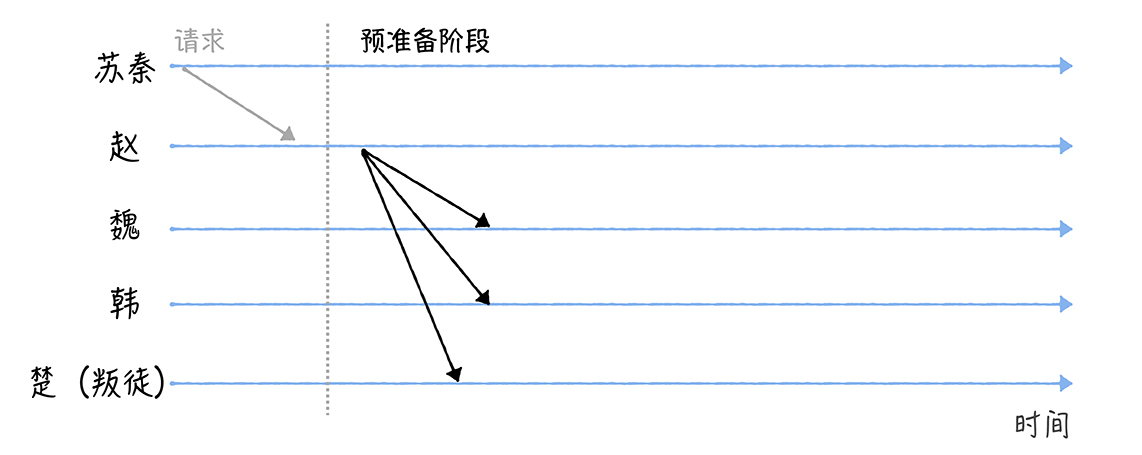
魏韩楚收到了消息,能够直接执行消息吗?
自然是不行的,因为无法确认彼此的消息是一致的吗,于是在进入准备阶段后进行了彼此的广播,各自广播准备消息给其他人
在这里,我们假设楚是通过不发送消息,来干扰共识协议
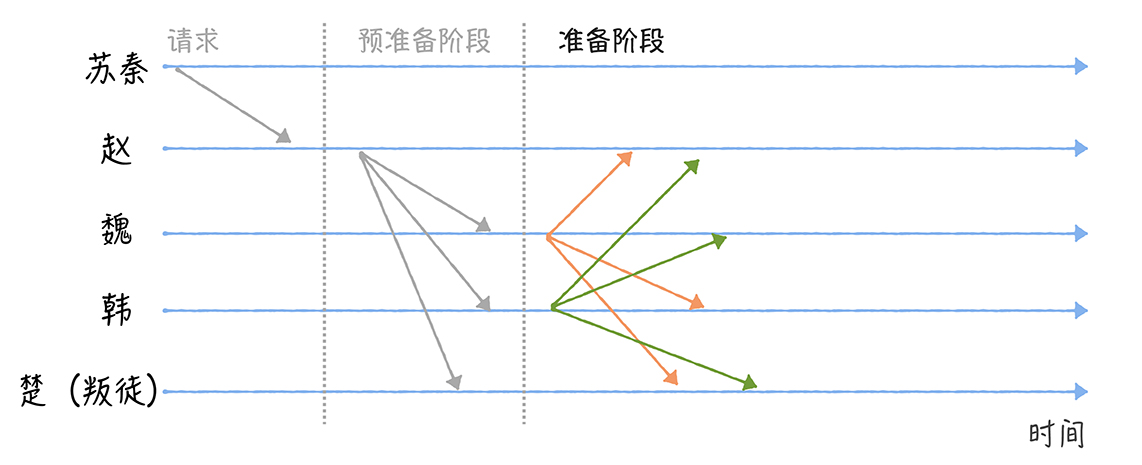
某个将军收到了2f (f是叛徒,我的演示是1)个作战指令的时候,会进入提交阶段,这时候先按兵不动,因为无法知道其他的赵韩楚是不是收到了一致的消息,这时候进入提交阶段
每个将军分别广播提交消息给其他的将军,告诉其他的将军,准备好了,可以执行指令了
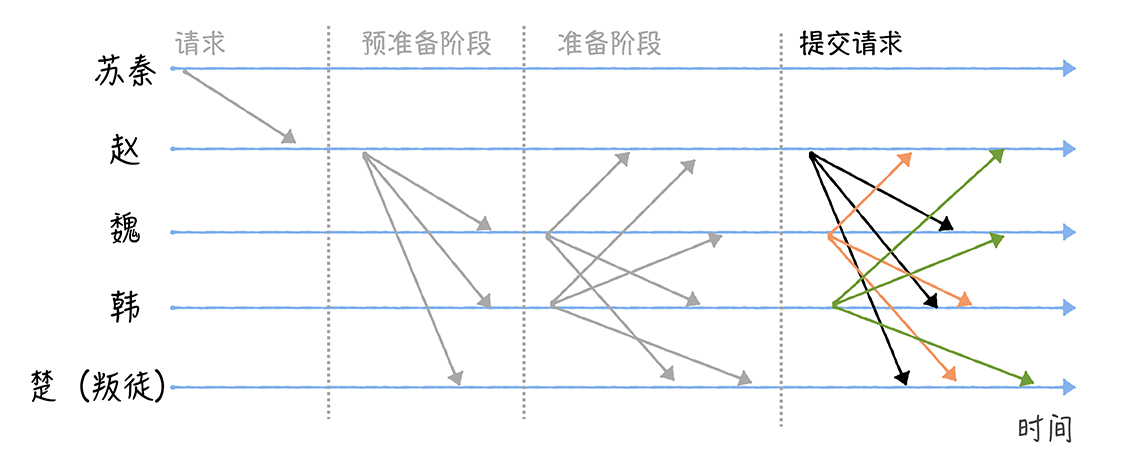
最后,当某个将军收到了2f+1个验证通过的消息后,这个+1是因为要算上自己,这时候就可以执行作战计划了,这个将军执行苏秦的作战指令,完成后,就将执行成功的消息发给苏秦
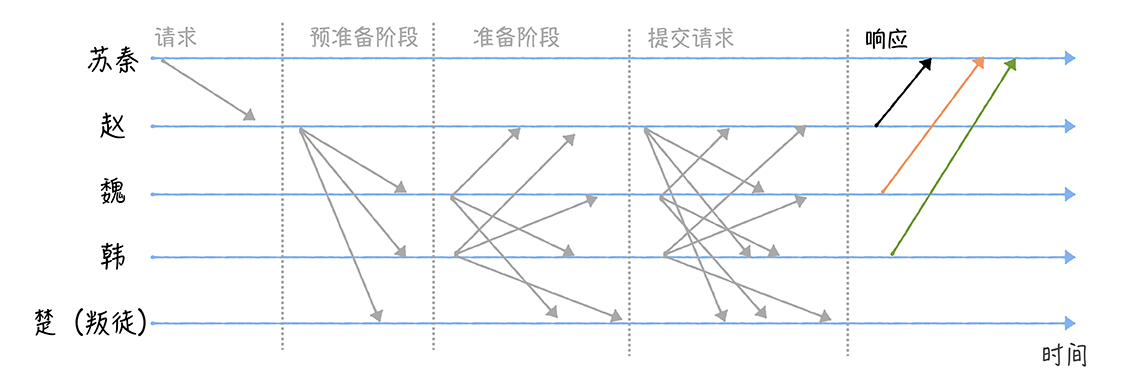
当苏苏秦收到了f+1个相同的相应信息的时候,就说明各个将军已经就作战指令完成了共识,执行了作战指令
这样,就完成了作战指令的统一化
这就是进行了达成统一化的作战指令,进行了作战指令的执行
这里,苏秦使用的就是简化的PBFT
首先,可以将赵魏韩楚认为是分布式系统的四个节点,赵是主节点,魏韩楚是备份节点
苏秦是客户端
进攻就是一个客户端的请求
总结一下,PBFT算法是通过签名来约束恶意节点的行为,也就是说每一个节点都可以去验证消息的来源,所以保证了可以基于大多数原则实现
而且,对于最终的共识是否达成了,客户端会记性判断,如果未收到f+1的相同响应,会认为出现了故障,从而重新发送
而且主节点是恶意节点的时候,会被发现,并且以轮流上岗的方式,推举新的节点
但是PBFT算法比起口信型拜占庭问题已经有了很大的优化,但是将消息的复杂度从O(n^(f+1))降低为了O(n^2),能够实际落地,解决实际的共识问题,但是还是有很多的消息
加入在13节点的集群中,我们有一个请求消息:1,叛徒是4
预准备消息:3f=12
准备消息:3f*(3f-f) = 96
提交消息是(3f-f+1) * (3f+1) = 117
回复消息 3f-1 = 11
这样一次的协商,需要237个消息,消息数还是很多的
按照上面的解法,不管是拜占庭的那种解法,都是非常理论化的,而且没有考虑到实际场景的需求,实现成本很高,难以解决实际的问题
PBFT算法是通过签名来约束恶意的节点的,采用三阶段协议,达成了一系列值的共识
仍然消息复杂度很高,因为存在一个领导者的节点,所以集群的性能取决于领导者节点,O(n^2)消息复杂度,随着消息数量增加,网络延迟必然增加,这就决定了PBFT算法适用于中小型的分布式系统
为何要收到f+1的结果吗
因为叛徒数是f个,如果只返回f个消息,那么可能存在返回的都是叛徒发送的错误消息,导致主节点认知错误,所以需要返回f+1,至于这个f,整篇文章说下来,感觉是一个不固定的值,实际上,应该是(n-1)/3,这一篇,实际上是第一篇拜占庭问题中签名解决方案的延伸,是吗