关于字符串的排序
我们会学习到高位优先排序(MSD)的字符串排序,类似于快速排序,都是对数组进行划分然后来然后递归的进行相同方法处理子数组
两者不同的是,快速排序会涉及所有的键,而高位优先排序则不需要,在切分的时候只需要检查键的第一个字符
但是在学习字符串的排序之前
先看一下基础,键索引计数法
用一个例子,就是进行分组——每个学生对应一个小组,将他们按照小组分开。在这个问题中,学生姓名就是字符串,而小组的组号就是对应的键值,我们需要将相同小组的同学分到一起(如图一)

我们假设每个学生都保存了一个名字和组号,我们使用a[i].key()来返回指定的学生组号
第一步:
使用int数组count来计数,对于数组中的每一个元素,都使用它的键来访问count[]中对应元素并使其+1,需要注意的是,如果键为r,那么则将count[r+]加一
第二步:
频率转换成索引,因为任意给定的键总是等于所有较小的键对应频率之和.对于每个键值r,小于r+1的键的频率之和为小于r的键的频率之和加上count[r]

第三步:
创建一个辅助数组aux[],每个元素在aux[]中的位置是由键的组别对应的count[]值决定的
在移动之后,count[]的对应元素+1,以保证下一个的位置
将索引进行了重排序
int N =a.length;//获取数组长度
String []aux = new String[N];//创建临时数组
int[] count = new int[R+1];//设置计数数组
for (int i = 0; i < N; i++) {
count[a[i].key()+1]++;//在计数数组中+1
}
for (int r = 0; r < R; r++) {
count[r+1] += count[r];//频率转换成索引
}
for (int i = 0; i < N; i++) {//每分类一个就将前面的空格填上一个
aux[count[a[i].key()]++] = a[i];
}
for (int i = 0; i < N; i++) {
a[i]=aux[i];
}
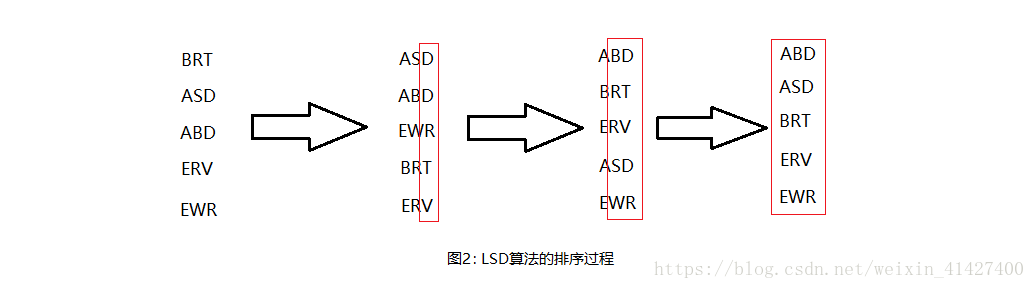
那么因此基础上,我们介绍一下低位优先排序 LSD
在字符串的长度相同的情况下,以右向左把每个字符作键,用键索计数法把字符串排序W遍
代码基本如下
|
public static void sort(String[] a,int w) {
int N = a.length;//获取数组长度,方便创建备份 int R = 256;//ASCII码大小 String[] aux = new String[N];//备份数组创建 for (int d = w -1; d>= 0; d–) {//第一层遍历 int[] count = new int[R+1];//计算出现频率 for (int i = 0; i < N; i++) {//遍历每个字符串的相同位置 count[a[i].charAt(d)+1]++;//获取频率 } for (int r = 0; r < R; r++) {//频率转换成索引 count[r+1]+=count[r]; } for (int r = 0; r < N; r++) {//元素分类 aux[count[a[r].charAt(d)]++] = a[r]; } for (int i = 0; i < N; i++) {//回写 a[i] = aux[i]; } } } |
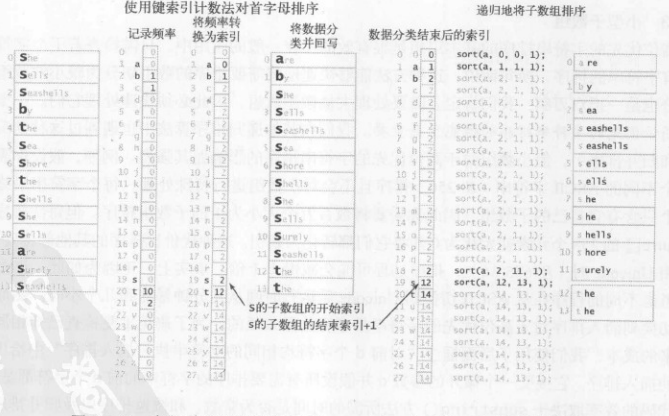
然后是高位优先的字符串排序
对于字符串的长度不确定的字符串,应该考虑从左向右遍历
称为高位优先,具体实现为先将首字母排序,然后按照首字母分成更小的子数组
对子数组进行排序
对于高位数组中可能存在的长度不同问题
可以将所有字符串都被检查过的字符串的子数组排在所有子数组之前
利用tochar的API,获取到一个数组索引,
然后在从数组中获取的时候,当指定的位置超过了字符串末尾返回-1,然后所有返回值+1,
0代表字符的结尾,1代表字母表的第一个字母
再加上检索计数法本身需要的一个额外位置,所以使用int count[] = new int[R+2]public static void sort(String[] a, int lo, int hi, int d) {
if (hi <= lo + M) {
// 转为插入排序,回来再补
return;
}
int[] count = new int[R + 2];// 计算频率的数组
for (int i = lo; i <= hi; i++) {// 计算频率
count[charAt(a[i], d) + 2]++;
}
for (int r = 0; r < R + 1; r++) {
count[r+1] += count[r];//转化索引
}
for (int r = 0; r<R;r++) {
aux[count[charAt(a[r], d)+1]++] = a[r];
}
for (int i = lo; i <= hi; i++) {
a[i]=aux[i];
}
for(int r = 0; r<R;r++) {
sort(a, lo+count[r], lo+count[r+1], d+1);
}
}
而且在最后的一个for循环中,我们尝试使用递归的方式,进行了递归的重排序

原本的子数组进行无阀值排序,会产生无数的微型小数组,而且每个数组都会重新将count[]的元素重新排序
故,如果字母表越大,可能占用内存越高