基础数学课19-特征转换
在本节中,我们说下特征工程中的另一个步骤,特征转换。
首先是为什么需要特征转换,我们之前介绍的监督式学习中,可以根据样本一系列特征,判断其属于哪个分类,这属于离散型的学习,但是除了这种离散型的预测之外,还有着连续性的模型供预测使用。比如我们需要根据历史的房地产销售数据,预测未来的一段时间走势。对于这种情况,我们称为因变量连续回归分析。
因变量连续回归分析的训练和预测和离散型的流程类似,就是研究多个随机变量y1 y2 y3和另一些变量x1 x2 x3之间的关系统计方法。
其中y1等称为因变量,x1等称为自变量。通常情况下,因变量的值可以分为两部分,一部分是自变量影响的函数,函数可能是线性或者非线形的。而除此外还有着随机误差。
如果因变量和自变量为线性关系的时候,就称为线性回归模型,如果是非线形的关系,就是非线形分析模型。
比如线形回归模型,基本形式为
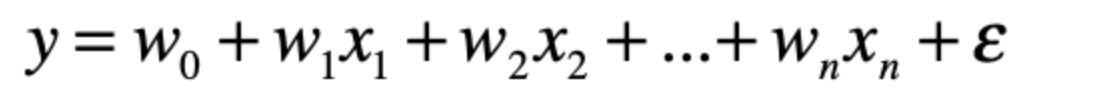
其中x为自变量,w为自变量的系数。ε是随机误差
对于w这个系数来说,可以是正的,也可以是负的。
如果某个系数大于0,表示是正向影响,自变量越大,结果就越大。否则就是负面影响。
那么这个w对线形回归模型来说,就很重要,对于如何计算w,我们先不说,我们先利用现有的线性回归模型,对历史房价数据进行一个回归分析。
| import pandas as pd
from sklearn.linear_model import LinearRegression df = pd.read_csv(“/Users/shenhuang/Data/boston-housing/train.csv”) #读取Boston Housing中的train.csv df_features = df.drop([‘medv’], axis=1) #Dataframe中除了最后一列,其余列都是特征,或者说自变量 df_targets = df[‘medv’] #Dataframe最后一列是目标变量,或者说因变量 regression = LinearRegression().fit(df_features, df_targets) #使用特征和目标数据,拟合线性回归模型 print(regression.score(df_features, df_targets)) #拟合程度的好坏 print(regression.coef_) #各个特征所对应的系 |
这样我们得到的结果中,首先是一个score值,表示的回归的拟合系数,如果越接近1,就说明越好。

其次就是不同的特征系数。其可以帮助我们解释哪个特征对最终的房价有较大的影响。
现在可以得到一个是3.78和3.87的最好,对应的是nox和age两个特征
Nox是空气污染,age是年龄。
从直接来看,nox作为主要影响房价的特征,确实不合适。
那么我们就需要进行特征变化方法,这里介绍两种,分别是归一化和标准化。
归一化就是获取原始数据的最大值和最小值。然后将所有的原始值变化到0-1之间
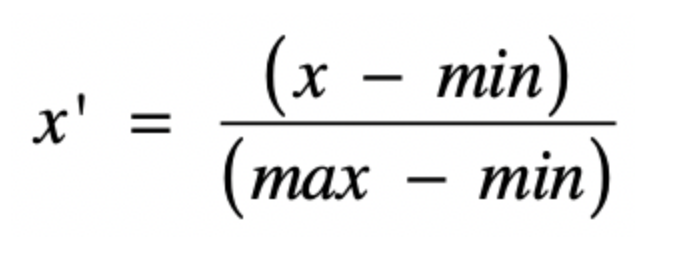
而这里,如果希望在线形回归之中使用归一化操作的话。也有着对应的函数

之后运行得到的结果,可以如下

其中拟合的分数没有变化,但是特征变化,这里的高分项是age和tax,也就是老房子和房产税影响比较高。这也是比较合适的。
标准化则是基于了正态分布进行的计算,也就是以中心点最高,然后不断的下降。其公式基本如下
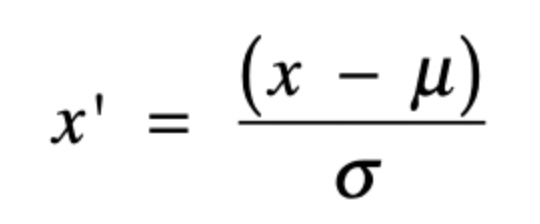
经过公式转换,所有高于的分数会得到一个正的标准分,负的分数会得到一个负的标准分数,并一定符合正态分布。
对应的使用也很简单

在训练之后,得到的结果为

其中表示高相关的特征还是age和tax,非常符合直觉。
总结一下,我们在这里说了下转换特征值,转移的原因在于不同类型的特征取值范围不同,分布也不同,相互之间没有可比性。所以需要转换。