基础数学课5-递归
这里我们讲述下递归
递归常用于一些保存大量的中间变量,如果直接使用循环的方式去保存的话,对于这些中间状态,并不好进行保存。而递归,其每次都进行的嵌套调用都可以保存自己的局部变量。
最终形成一个如下的图
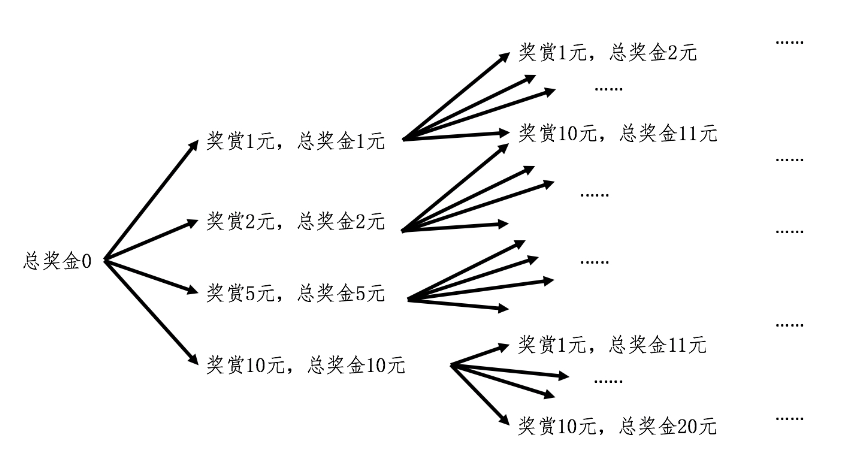
在这个图中,我们并没有体现出当递归到最终的结果的时候,该如何解决问题呢?
就比如我们的入口是对n等于k的时候进行向下递归,这样n不断的减少,直到n=1的时候,就是递归的尽头,如果递归到了尽头,常见的方式是返回一个固定值,然后不断的回滚,汇总到n=k的时候。
也就是说,将复杂的问题,不断的进行简化,简化为更为简单的问题进行求解。直到最简单的形式。
| import java.util.ArrayList;
public class Lesson5 { public static long[] rewards = {1, 2, 5, 10}; // 四种面额的纸币 /** * @param totalReward-奖赏总金额,result+保存当前的解 * @return void * @Description: 使用函数的递归(嵌套)调用,找出所有可能的奖赏组合 */ public static void get(long totalReward, ArrayList<Long> result) { // 当totalReward = 10时,证明它是满足条件的解,结束嵌套调用,输出解 if (totalReward == 10) { System.out.println(result); return; } // 当totalReward > 10时,证明它不是满足条件的解,不输出 else if (totalReward > 10) { return; } else { for (int i = 0; i < rewards.length; i++) { ArrayList<Long> newResult = (ArrayList<Long>) (result.clone()); // 由于有4种情况,需要clone当前的解并传入被调用的函数 newResult.add(rewards[i]); // 记录当前的选择,解决一点问题 get(totalReward + rewards[i], newResult); // 剩下的问题,留给嵌套调用去解决 } } } } |
比如上面的,这样我们就通过递归的方式,展示了所有可行的组合方式
而在计算机领域,递归更多的场景是面向分治的领域进行处理。
在计算机中,分治往往面对的问题是可以将一个巨大的问题不断的拆分为小问题,并进行计算的人物,常见的就是归并排序。
比如我们需要对一个数组进行排序,那么一种办法就是不断的将数组拆分,直到拆分到一个值,然后不断的合并,通过保证小数组有序,从而在上层合并的时候,通过已经有序的两个子数组,从而加快排序顺序
所以这个算法,就是将长度为n的数列,每次简化为长度为n-1的数列,直到长度为1,然后不断的合并
在这个算法中,我们就说明了分而治之的思想,分而治之,就是将一个复杂的问题,分解为两个或多个子问题,子问题递归式的细分,直到问题很简单, 可以被求解。
后来引入到分布式系统中, 就比如要对一个大型的数据进行排序,比如1024G,超过了单台机器性能上线,是否就可以引入分治,将其分解为更小的数据集,分配到其他机器上,并行的处理,处理完成进行汇总。最后进行合并返回 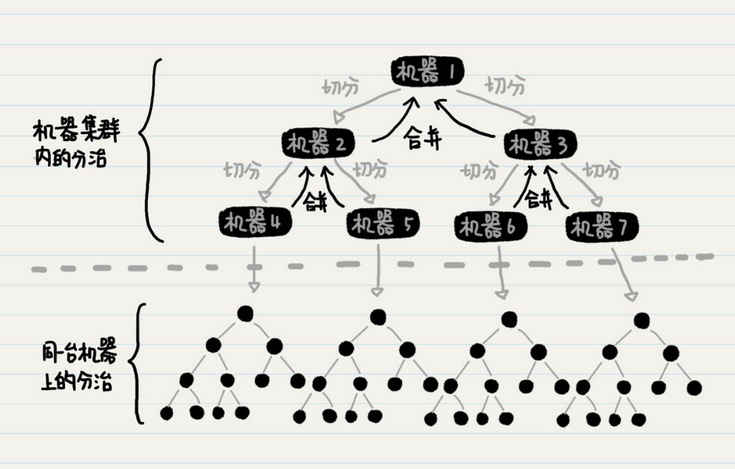
上面的图就是简单的归并的实现
当然在实际的实现过程中,不会出现上图中机器2 机器3 不承担计算任务的情况
可能是机器2自身承担一部分计算,然后将另一部分继续下发。
那么我们总结下分治
分治需要经过三个阶段
分别是数据分割和映射
归约
合并
这三个步骤,最终实现了机器的分治合并。
因为分治,这也是为什么我们需要学习递归的原因。